题目内容
已知菱形ABCD中,AB=2,∠A=120°,沿对角线BD将△ABD折起,使二面角A-BD-C为120°,则点A到△BCD所在平面的距离等于( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:先在三角形ABD中求出AO=1;然后过A作面BCD的垂线,垂足E,则AE即为所求;最后在RT△AOE中,求出AE即可得出结论.
解答: 解:设AC与BD交于点O.
解:设AC与BD交于点O.
在三角形ABD中,因为∠A=120°,AB=2.可得AO=1.
过A作面BCD的垂线,垂足E,则AE即为所求.
由题得,∠AOE=180°-∠AOC=180°-120°=60°.
在RT△AOE中,AE=AO•sin∠AOE=
.
故选:D.
 解:设AC与BD交于点O.
解:设AC与BD交于点O.在三角形ABD中,因为∠A=120°,AB=2.可得AO=1.
过A作面BCD的垂线,垂足E,则AE即为所求.
由题得,∠AOE=180°-∠AOC=180°-120°=60°.
在RT△AOE中,AE=AO•sin∠AOE=
| ||
| 2 |
故选:D.
点评:本题主要考查点到面的距离计算以及折叠问题.在解决折叠问题时,一定要注意分析出哪些量发生了变化,又有哪些量没有发生变化.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目

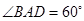 (如图1所示),将菱形ABCD沿对角线
(如图1所示),将菱形ABCD沿对角线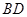 翻折,使点
翻折,使点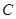 翻折到点
翻折到点 的位置(如图2所示),点E,F,M分别是AB,DC1,BC1的中点.
的位置(如图2所示),点E,F,M分别是AB,DC1,BC1的中点.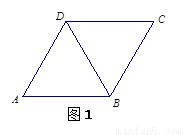

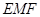 ;
;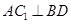
 时,求线段AC1 的长.
时,求线段AC1 的长.