题目内容
已知菱形ABCD中,AB=2,∠A=120°,沿对角线BD将△ABD折起,使二面角A-BD-C为120°,则点A到△BCD所在平面的距离等于分析:本题考查了立体几何中的折叠问题,及定义法求二面角和点到平面的距离,我们由已知菱形ABCD中,AB=2,∠A=120°,沿对角线BD将△ABD折起,使二面角A-BD-C为120°,及菱形的性质:对角线互相垂直,我们易得∴∠AOC即为二面角A-BD-C的平面角,解△AOC后,OC边的高即为A点到平面BCD的距离.
解答: 解:已知如下图所示:
解:已知如下图所示:
设AC∩BD=O,则AO⊥BD,CO⊥BD,
∴∠AOC即为二面角A-BD-C的平面角
∴∠AOC=120°,且AO=1,
∴d=1×sin60°=
故答案为:
 解:已知如下图所示:
解:已知如下图所示:设AC∩BD=O,则AO⊥BD,CO⊥BD,
∴∠AOC即为二面角A-BD-C的平面角
∴∠AOC=120°,且AO=1,
∴d=1×sin60°=
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:根据二面角的大小解三角形,一般先作出二面角的平面角.此题是利用二面角的平面角的定义作出∠AOC为二面角A-BD-C的平面角,通过解∠AOC所在的三角形求得∠AOC.其解题过程为:作∠AOC→证∠AOC是二面角的平面角→利用∠AOC解三角形AOC,简记为“作、证、算”.

练习册系列答案
相关题目

 (如图1所示),将菱形ABCD沿对角线
(如图1所示),将菱形ABCD沿对角线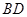 翻折,使点
翻折,使点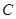 翻折到点
翻折到点 的位置(如图2所示),点E,F,M分别是AB,DC1,BC1的中点.
的位置(如图2所示),点E,F,M分别是AB,DC1,BC1的中点.

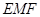 ;
;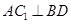
 时,求线段AC1 的长.
时,求线段AC1 的长.