题目内容
6．
某校某年级有100名学生，已知这些学生完成家庭作业的时间均在区间[0.5，3.5）内（单位：小时），现将这100人完成家庭作业的时间分为3组：[0.5，1.5），[1.5，2.5），[2.5，3.5）加以统计，得到如图所示的频率分布直方图．在这100人中，采用分层抽样的方法抽取10名学生研究其视力状况与完成作业时间的相关性，则在抽取样本中，完成作业的时间超过1.5个小时的有5人．
分析 根据频率分布直方图，利用频率、频数与样本容量的关系即可求出结果．
解答 解：根据频率分布直方图得，完成作业的时间超过1.5个小时的频率为：
0.4+0.1=0.5，
所以应抽取的学生是10×0.5=5人．
故答案为：5．
点评 本题考查了频率分布直方图的应用问题，是基础题目．
练习册系列答案
相关题目
16．
在四棱锥P-ABCD中，底面ABCD是一直角梯形，BA⊥AD，AD∥BC，AB=BC=2，PA=3，PA⊥底面ABCD，E是棱PD上异于P，D的动点．设$\frac{PE}{ED}$=m，则“0＜m＜2”是三棱锥C-ABE的体积不小于1的（ ）
在四棱锥P-ABCD中，底面ABCD是一直角梯形，BA⊥AD，AD∥BC，AB=BC=2，PA=3，PA⊥底面ABCD，E是棱PD上异于P，D的动点．设$\frac{PE}{ED}$=m，则“0＜m＜2”是三棱锥C-ABE的体积不小于1的（ ）| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
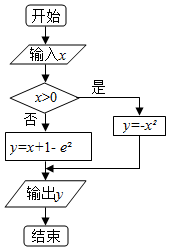
14．运行如图程序框图，则当输出y的值最大时，输入的x值等于（ ）
| A． | 0 | B． | 1 | C． | -1 | D． | 2 |
1．已知命题p，q，则“￢p或q为假”是“p且￢q为真”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
11．$\int_0^1{|x-1|}dx$=（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | $\frac{1}{2}$ |
15．已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π）的图象与x轴的一个交点$（-\frac{π}{12}，0）$到其相邻的一条对称轴的距离为$\frac{π}{4}$．若$f（\frac{π}{12}）=\frac{3}{2}$，则函数f（x）在$[0，\frac{π}{2}]$上的最小值为（ ）
| A． | $\frac{1}{2}$ | B． | $-\sqrt{3}$ | C． | $-\frac{{\sqrt{3}}}{2}$ | D． | $-\frac{1}{2}$ |