题目内容
18.设直线y=t与曲线C:y=x(x-3)2的三个交点分别为A(a,t),B(b,t),C(c,t),且a<b<c.现给出如下结论:①abc的取值范围是(0,4);
②a2+b2+c2为定值;
③c-a有最小值无最大值.
其中正确结论的个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 作出f(x)=x(x-3)2的函数图象,判断t的范围,根据f(x)的变化率判断c-a的变化情况,构造函数g(x)=x(x-3)2-t,根据根与系数的关系得出abc,a2+b2+c2,c-a的值进行判断.
解答 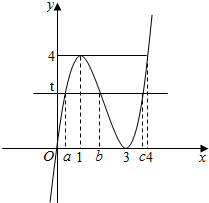 解:令f(x)=x(x-3)2=x3-6x2+9x,f′(x)=3x2-12x+9,令f′(x)=0得x=1或x=3.
解:令f(x)=x(x-3)2=x3-6x2+9x,f′(x)=3x2-12x+9,令f′(x)=0得x=1或x=3.
当x<1或x>3时,f′(x)>0,当1<x<3时,f′(x)<0.
∴f(x)在(-∞,1)上是增函数,在(1,3)上是减函数,在(3,+∞)上是增函数,
当x=1时,f(x)取得极大值f(1)=4,当x=3时,f(x)取得极小值f(3)=0.
作出函数f(x)的图象如图所示:
∵直线y=t与曲线C:y=x(x-3)2有三个交点,∴0<t<4.
令g(x)=x(x-3)2-t=x3-6x2+9x-t,则a,b,c是g(x)的三个实根.
∴abc=t,a+b+c=6,ab+bc+ac=9,
∴a2+b2+c2=(a+b+c)2-2(ab+bc+ac)=18.
由函数图象可知f(x)在(0,1)上的变化率逐渐减小,在(3,4)上的变化率逐渐增大,
∴c-a的值先增大后减小,故c-a存在最大值,不存在最小值.
故①,②正确,
故选:C.
点评 本题考查了导数与函数的单调性,函数的图象,三次方程根与系数的关系,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.对任意x∈[-1,1],不等式-4≤x3+3|x-a|≤4恒成立,则实数a的取值范围为( )
| A. | [-$\frac{2}{3}$,$\frac{2}{3}$] | B. | [-$\frac{1}{3}$,$\frac{1}{3}$] | C. | [0,$\frac{2}{3}$] | D. | [0,1] |
8.已知f(x)=$\left\{\begin{array}{l}{sinπx,x≤0}\\{2f(x-1),x>0}\end{array}\right.$,则f($\frac{4}{3}$)等于( )
| A. | 2 | B. | -2 | C. | 2$\sqrt{3}$ | D. | -2$\sqrt{3}$ |