题目内容
设数列{an}的前n项和为Sn,并且满足2Sn=a +n,an>0(n∈N*).
+n,an>0(n∈N*).
(1)猜想{an}的通项公式,并用数学归纳法加以证明.
(2)设x>0,y>0,且x+y=1,证明: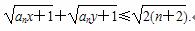
(1)分别令n=1,2,3,
得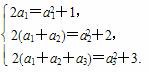
∵an>0,∴a1=1,a2=2,a3=3.
猜想:an=n.
由2Sn=a +n.①
+n.①
可知,当n≥2时,2Sn-1=a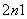 +(n-1).②
+(n-1).②
①-②,得2an=a -a
-a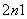 +1,
+1,
即a =2an+a
=2an+a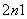 -1.
-1.
(ⅰ)当n=2时,a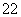 =2a2+12-1,
=2a2+12-1,
∵a2>0,∴a2=2.
(ⅱ)假设当n=k(k≥2)时,ak=k,那么当n=k+1时,
a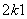 =2ak+1+a
=2ak+1+a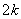 -1=2ak+1+k2-1
-1=2ak+1+k2-1
⇒[ak+1-(k+1)][ak+1+(k-1)]=0,
∵ak+1>0,k≥2,∴ak+1+(k-1)>0,
∴ak+1=k+1.
即当n=k+1时也成立.
∴an=n(n≥2).
显然n=1时,也成立,故对于一切n∈N*,均有an=n.
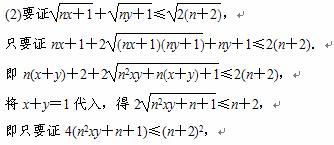 即4xy≤1.
即4xy≤1.
∵x>0,y>0,且x+y=1,∴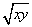 ≤
≤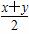 =
= ,
,
即xy≤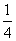 ,故4xy≤1成立,所以原不等式成立.
,故4xy≤1成立,所以原不等式成立.

练习册系列答案
相关题目
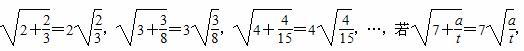 (a、t均为正实数),则类比以上等式,可推测a、t的值,a+t=( )
(a、t均为正实数),则类比以上等式,可推测a、t的值,a+t=( )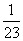 +
+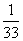 +
+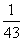 +…+
+…+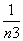 ,g(n)=
,g(n)=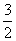 -
-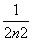 ,n∈N*.
,n∈N*.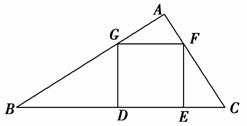

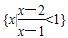 ,则M∩N等于( )
,则M∩N等于( )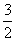 } B.{x|
} B.{x| <x<1}
<x<1}