题目内容
11.若向量$\overrightarrow{a}$,$\overrightarrow{b}$满足$|a|=2,|b|=\sqrt{3}$,且$\overrightarrow{b}$⊥($\overrightarrow{a}$+$\overrightarrow{b}$)则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
分析 根据$\overrightarrow{b}⊥(\overrightarrow{a}+\overrightarrow{b})$即可得到$\overrightarrow{b}•(\overrightarrow{a}+\overrightarrow{b})=0$,进行数量积的运算便可求出$cos<\overrightarrow{a},\overrightarrow{b}>=-\frac{\sqrt{3}}{2}$,从而求出向量$\overrightarrow{a},\overrightarrow{b}$的夹角.
解答 解:∵$\overrightarrow{b}⊥(\overrightarrow{a}+\overrightarrow{b})$;
∴$\overrightarrow{b}•(\overrightarrow{a}+\overrightarrow{b})=\overrightarrow{a}•\overrightarrow{b}+{\overrightarrow{b}}^{2}$
=$2\sqrt{3}cos<\overrightarrow{a},\overrightarrow{b}>+3$
=0;
∴$cos<\overrightarrow{a},\overrightarrow{b}>=-\frac{\sqrt{3}}{2}$;
∵$\overrightarrow{a}$与$\overrightarrow{b}$夹角的取值范围为[0,π],
∴$\overrightarrow{a},\overrightarrow{b}$的夹角为$\frac{5π}{6}$.
故选:D.
点评 考查向量垂直的充要条件,向量数量积的运算及计算公式,以及向量夹角的范围.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.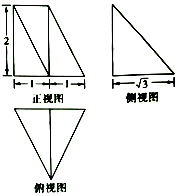 某几何体的三视图如图所示,则该几何体的体积为( )
某几何体的三视图如图所示,则该几何体的体积为( )
 某几何体的三视图如图所示,则该几何体的体积为( )
某几何体的三视图如图所示,则该几何体的体积为( )| A. | 3$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $\frac{4}{3}$$\sqrt{3}$ | D. | $\frac{5}{3}$$\sqrt{3}$ |
6.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左顶点为A,右焦点为F(c,0),直线x=c与双曲线C在第一象限的交点为P,过F的直线l与双曲线C过二、四象限的渐近线平行,且与直线AP交于点B,若△ABF与△PBF的面积的比值为2,则双曲线C的离心率为( )
| A. | $\frac{5}{3}$ | B. | $\frac{3\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
1.函数f(x)=$\frac{1}{1+{x}^{2}}$的值域是( )
| A. | {y|y≠0} | B. | (0,1] | C. | (0,1) | D. | [1,+∞) |