题目内容
(本小题满分14分)已知函数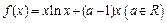 .
.
(Ⅰ)当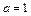 时,求曲线
时,求曲线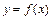 在
在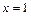 处的切线方程;
处的切线方程;
(Ⅱ)求函数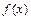 在区间
在区间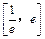 上的最小值;
上的最小值;
(Ⅲ)若关于的方程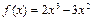 在区间
在区间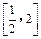 内有两个不相等的实数根,求实数a的取值范围.
内有两个不相等的实数根,求实数a的取值范围.
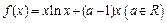 .
.(Ⅰ)当
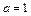 时,求曲线
时,求曲线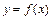 在
在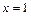 处的切线方程;
处的切线方程;(Ⅱ)求函数
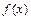 在区间
在区间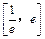 上的最小值;
上的最小值;(Ⅲ)若关于的方程
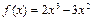 在区间
在区间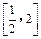 内有两个不相等的实数根,求实数a的取值范围.
内有两个不相等的实数根,求实数a的取值范围.解:(Ⅰ) ∵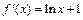 ,∴
,∴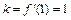 ,
,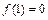 ,
,
∴所求的切线方程为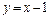 . ………………………………………………3分
. ………………………………………………3分
(Ⅱ)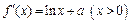 .
.
由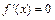 得
得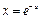 .
.
①当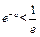 ,即
,即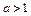 时,
时,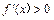 ,
,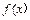 在
在 上为增函数,
上为增函数,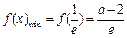 ;
;
②当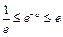 ,即
,即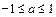 时,在
时,在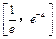 上
上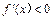 ,
,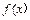 为减函数,在
为减函数,在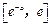 上
上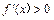 ,
,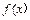 为增函数,
为增函数,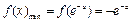 ;
;
③当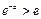 ,即
,即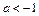 时,
时,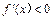 ,
,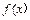 在
在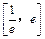 上为减函数,
上为减函数,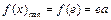 .
.
…………………………8分
综上所述,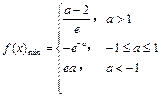 . ……………………………9分
. ……………………………9分
(Ⅲ)∵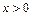 ,方程:
,方程: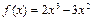 在
在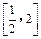 上有两个不相等的实数根,
上有两个不相等的实数根,
等价于方程: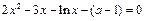 在
在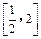 上有两个不相等的实数根.
上有两个不相等的实数根.
令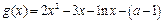 ,则
,则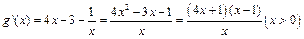 ,
,
令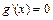 ,得
,得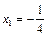 (舍去),
(舍去),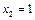 ,因此
,因此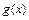 在
在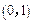 内是减函数,在
内是减函数,在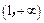 内是增函数,因此,方程
内是增函数,因此,方程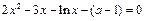 在
在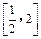 内有两个不相等的实数根,只需方程:
内有两个不相等的实数根,只需方程:
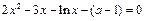 在
在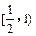 和
和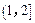 内各有一个实根,
内各有一个实根,
于是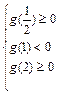 ,解得
,解得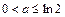 ,
,
∴a的取值范围是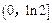 . …………………………14分
. …………………………14分
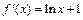 ,∴
,∴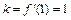 ,
,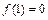 ,
,∴所求的切线方程为
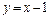 . ………………………………………………3分
. ………………………………………………3分(Ⅱ)
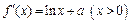 .
.由
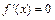 得
得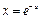 .
.①当
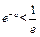 ,即
,即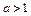 时,
时,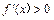 ,
,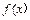 在
在 上为增函数,
上为增函数,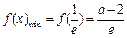 ;
;②当
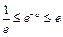 ,即
,即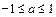 时,在
时,在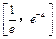 上
上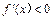 ,
,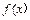 为减函数,在
为减函数,在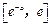 上
上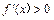 ,
,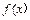 为增函数,
为增函数,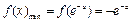 ;
;③当
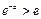 ,即
,即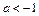 时,
时,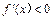 ,
,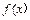 在
在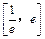 上为减函数,
上为减函数,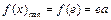 .
.…………………………8分
综上所述,
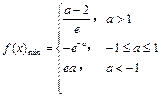 . ……………………………9分
. ……………………………9分(Ⅲ)∵
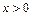 ,方程:
,方程: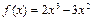 在
在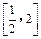 上有两个不相等的实数根,
上有两个不相等的实数根,等价于方程:
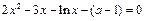 在
在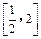 上有两个不相等的实数根.
上有两个不相等的实数根.令
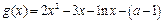 ,则
,则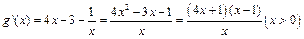 ,
,令
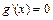 ,得
,得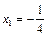 (舍去),
(舍去),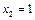 ,因此
,因此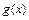 在
在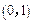 内是减函数,在
内是减函数,在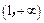 内是增函数,因此,方程
内是增函数,因此,方程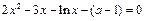 在
在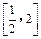 内有两个不相等的实数根,只需方程:
内有两个不相等的实数根,只需方程: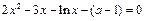 在
在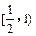 和
和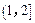 内各有一个实根,
内各有一个实根,于是
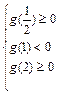 ,解得
,解得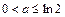 ,
,∴a的取值范围是
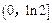 . …………………………14分
. …………………………14分略

练习册系列答案
相关题目
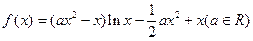 .
.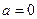 时,求曲线
时,求曲线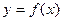 在
在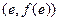 处的切线方程(
处的切线方程(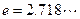 )
)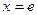 为函数
为函数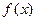 的极值点,求函数
的极值点,求函数 的单调区间。
的单调区间。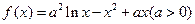 (Ⅰ)求
(Ⅰ)求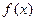 单调区间(Ⅱ)求所有实数
单调区间(Ⅱ)求所有实数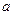 ,使
,使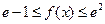 对
对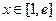 恒成立
恒成立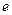 为自然对数的底数
为自然对数的底数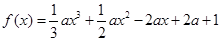 的图象经过四个象限,则实数
的图象经过四个象限,则实数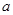 的取值范围是( )
的取值范围是( ) 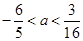
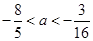
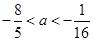
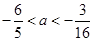
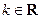 函数
函数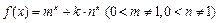 .
.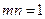 且函数
且函数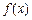 为奇函数,求实数
为奇函数,求实数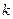 ;
; 试判断函数
试判断函数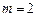 ,
,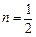 ,
,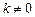 时,求函数
时,求函数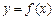 的对称轴或对称中心.
的对称轴或对称中心.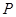 是曲线
是曲线 上的一个动点,则点
上的一个动点,则点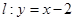 的距离的最小值为( )
的距离的最小值为( )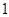
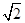
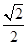
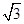
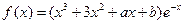 .
.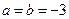 时,求
时,求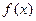 的单调区间;
的单调区间;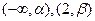 单调增加,在
单调增加,在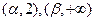 单调减少,证明:
单调减少,证明: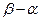 <6.
<6.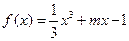 ,
,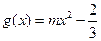
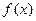 的单调性;
的单调性;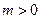 且函数
且函数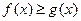 在
在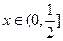 上有解,求
上有解,求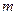 的范围.
的范围.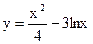 的一条切线的斜率为
的一条切线的斜率为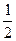 ,则切点的纵坐标为 ▲
,则切点的纵坐标为 ▲