��Ŀ����
4������������������2015��11��10������6ʱ�����˵�AQI����������ָ�����ﵽ290�������ض���Ⱦ����Ϊ����Ϊ74������PM2.5��ϸ��������ݳ����п����������ij��У������������̲��ݻ���ij��λ�ڹ��ҿ��в��ŵ�֧���£����м������أ��������¹��գ�����ϸ��������д�������֪�õ�λÿ�µĴ���������Ϊ300�֣����Ϊ600�֣��´����ɱ�y��Ԫ�����´�����x���֣�֮��ĺ�����ϵ�ɽ��Ƶı�ʾΪy=$\frac{1}{2}$x2-200x+80000����ÿ��ϸ�������ƽ�������ɱ����Ϊ��������| A�� | 100Ԫ | B�� | 200Ԫ | C�� | 300Ԫ | D�� | 400Ԫ |
���� ͨ����ÿ��ϸ�������ƽ�������ɱ�t��x��=$\frac{y}{x}$�����֪t��x��=$\frac{1}{2}$x+$\frac{80000}{x}$-200�����û�������ʽ���㼴�ý��ۣ�
��� �⣺�����⣬300��x��600����ÿ��ϸ�������ƽ�������ɱ�Ϊt��x����
��t��x��=$\frac{y}{x}$=$\frac{\frac{1}{2}{x}^{2}-200x+80000}{x}$=$\frac{1}{2}$x+$\frac{80000}{x}$-200��
��$\frac{1}{2}$x+$\frac{80000}{x}$��2$\sqrt{\frac{x}{2}•\frac{80000}{x}}$=400��
���ҽ���$\frac{1}{2}$x=$\frac{80000}{x}$��x=400ʱȡ�Ⱥţ�
�൱x=400ʱt��x��ȡ��Сֵ400-200=200��Ԫ����
��ѡ��B��
���� ���⿼�麯��ģ�͵�ѡ����Ӧ�ã������������ʽ��ע����ⷽ���Ļ��ۣ������е��⣮

��ϰ��ϵ�д�
 �п�������㾫��ϵ�д�
�п�������㾫��ϵ�д� ������ĩ��ϰ��ѵ��ϵ�д�
������ĩ��ϰ��ѵ��ϵ�д�
�����Ŀ
15��ֱ��ax+by-a-b=0��a�٣���Բx2+y2-2=0��λ�ù�ϵΪ��������
| A�� | ���� | B�� | ���� | C�� | �ཻ������ | D�� | �ཻ |
12����ͼ����Բһ���ֺ��ķ�֮һ����ɵ�����������ͼ����˼���������Ϊ��������
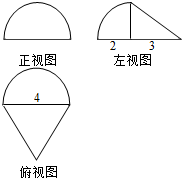

| A�� | $\frac{8��}{3}$ | B�� | $\frac{16��}{3}$ | C�� | $\frac{14��}{3}$ | D�� | $\frac{2��}{3}$ |
19����ԭ���ֱ����˫����$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$��a��0��b��0������M��N���㣬P��˫����������M��N��һ�㣬��ֱ��MP��ֱ��NP��б�ʶ������ҳ˻�Ϊ$\frac{5}{4}$����˫���ߵ�������Ϊ��������
| A�� | $\frac{3}{2}$ | B�� | $\frac{9}{4}$ | C�� | $\frac{5}{4}$ | D�� | 2 |
9��ִ����ͼ��ʾ�ij����ͼ���������x=4.5���������i=��������


| A�� | 3 | B�� | 4 | C�� | 5 | D�� | 6 |
16���Ķ���ͼ���㷨��ͼ������Ľ��S��ֵΪ��������
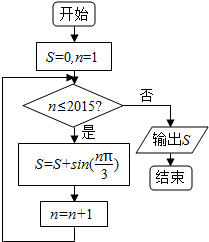

| A�� | $\frac{{\sqrt{3}}}{2}$ | B�� | 0 | C�� | $\sqrt{3}$ | D�� | $-\frac{{\sqrt{3}}}{2}$ |
13��ij�����������ͼ��ͼ��ʾ����ü�����������ı����Ϊ��������


| A�� | 8�� | B�� | 16�� | C�� | 32�� | D�� | 64�� |