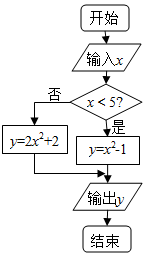
题目内容
11.函数y=sin(2x+φ)的图象沿x轴向左平移$\frac{π}{8}$个单位后,得到一个偶函数的图象,设φ取最小正值时所得偶函数为g(x),则函数y=x2g(x)的部分图象可以为( )| A. |  | B. |  | C. |  | D. |  |
分析 根据三角函数的图象平移关系以及函数奇偶性的性质求出函数g(x)的表达式,结合函数的图象的性质进行判断即可.
解答 解:函数y=sin(2x+φ)的图象沿x轴向左平移$\frac{π}{8}$个单位后得到y=sin[2(x+$\frac{π}{8}$)+φ]=sin(2x+$\frac{π}{4}$+φ),
若函数为偶函数,
则$\frac{π}{4}$+φ=$\frac{π}{2}$+kπ,
则φ=kπ+$\frac{π}{4}$,
当k=0时,φ取的最小正值,为φ=$\frac{π}{4}$,
则g(x)=sin(2x+$\frac{π}{4}$+$\frac{π}{4}$)=cos2x,
则y=x2g(x)=y=x2cos2x,
则函数为偶函数,图象关于y轴对称,则排除A,B,
当x=0时,y=0,排除D,
故选:C.
点评 本题主要考查函数图象的识别和判断,根据三角函数的图象和性质求出函数g(x)的解析式是解决本题的关键.利用特殊值法和排除法是解决函数图象常用的方法.

练习册系列答案
相关题目
1. 函数f(x)=Asin(ωx+φ)(A>0,ω>0)的图象如图所示.为了得到g(x)=-Acosωx(A>0,ω>0)的图象,可以将f(x)的图象( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0)的图象如图所示.为了得到g(x)=-Acosωx(A>0,ω>0)的图象,可以将f(x)的图象( )
 函数f(x)=Asin(ωx+φ)(A>0,ω>0)的图象如图所示.为了得到g(x)=-Acosωx(A>0,ω>0)的图象,可以将f(x)的图象( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0)的图象如图所示.为了得到g(x)=-Acosωx(A>0,ω>0)的图象,可以将f(x)的图象( )| A. | 向右平移$\frac{π}{12}$个单位长度 | B. | 向右平移$\frac{5π}{12}$个单位长度 | ||
| C. | 向左平移$\frac{π}{12}$个单位长度 | D. | 向左平移$\frac{5π}{12}$个单位长度 |
2.若a为实数且(2+ai)(a-2i)=8,则a=( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
6.设向量$\vec a$与$\vec b$满足:$\vec b$在$\vec a$方向上的投影为1,$\vec a$与$\vec a-2\vec b$垂直,则$|{\vec a}|$=( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 3 |
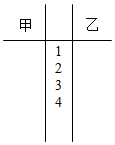 某苗圃基地为了解基地内甲、乙两块地种植的同一种树苗的长势情况,从两块地各随机抽取了10株树苗,分别测出它们的高度如下(单位:cm)
某苗圃基地为了解基地内甲、乙两块地种植的同一种树苗的长势情况,从两块地各随机抽取了10株树苗,分别测出它们的高度如下(单位:cm)