题目内容
16.函数f(x)=sin(2x+φ)(|φ|<π)的图象向左平移$\frac{π}{6}$个单位后关于原点对称,则φ=-$\frac{π}{3}$或$\frac{2π}{3}$.分析 根据三角函数的图象平移关系,结合三角函数的奇偶性进行求解即可.
解答 解:将f(x)=sin(2x+φ)(|φ|<π)的图象向左平移$\frac{π}{6}$个单位,
得到y=sin[2(x+$\frac{π}{6}$)+φ]=sin(2x+$\frac{π}{3}$+φ),
若此时函数关于原点对称,
则$\frac{π}{3}$+φ=kπ,
即φ=-$\frac{π}{3}$+kπ,
∵|φ|<π,
∴当k=0时,φ=-$\frac{π}{3}$,
若k=1时,φ=-$\frac{π}{3}$+π=$\frac{2π}{3}$,
故答案为:-$\frac{π}{3}$或$\frac{2π}{3}$
点评 本题主要考查三角函数的图象关系以及三角函数的性质,利用三角函数奇偶性的性质是解决本题的关键.

练习册系列答案
相关题目
6.已知复数z满足z=(1+i)(2-i)i(其中i为虚数单位),则$\overrightarrow{z}$在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
7.已知集合M={x|x2>1},N={-2,-1,0,1,2},则M∩N=( )
| A. | {0} | B. | {2} | C. | {-2,-1,1,2} | D. | {-2,2} |
4.若复数$z=\frac{1-3i}{1+i}$,则|z+1|=( )
| A. | 3 | B. | 2 | C. | $\sqrt{2}$ | D. | $\sqrt{5}$ |
11.函数y=sin(2x+φ)的图象沿x轴向左平移$\frac{π}{8}$个单位后,得到一个偶函数的图象,设φ取最小正值时所得偶函数为g(x),则函数y=x2g(x)的部分图象可以为( )
| A. |  | B. |  | C. |  | D. |  |
6.为了解学生暑假阅读名著的情况,一名教师对某班级的所有学生进行了调查,调查结果如表.
(Ⅰ)从这班学生中任选一名男生,一名女生,求这两名学生阅读名著本数之和为4的概率?
(Ⅱ)若从阅读名著不少于4本的学生中任选4人,设选到的男学生人数为X,求随机变量X的分布列和数学期望;
(Ⅲ)试判断男学生阅读名著本数的方差${s_1}^2$与女学生阅读名著本数的方差${s_2}^2$的大小(只需写出结论).
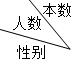 | 1 | 2 | 3 | 4 | 5 |
| 男生 | 1 | 4 | 3 | 2 | 2 |
| 女生 | 0 | 1 | 3 | 3 | 1 |
(Ⅱ)若从阅读名著不少于4本的学生中任选4人,设选到的男学生人数为X,求随机变量X的分布列和数学期望;
(Ⅲ)试判断男学生阅读名著本数的方差${s_1}^2$与女学生阅读名著本数的方差${s_2}^2$的大小(只需写出结论).