题目内容
16.在平面直角坐标系xOy中,将函数y=$\sqrt{3+2x-{x}^{2}}$-$\sqrt{3}$(x∈[0,2])的图象绕坐标原点O按逆时针方向旋转角θ,若?θ∈[0,a],旋转后所得的曲线都是某个函数的图象,则a的最大值为60°.分析 确定函数在x=0处,函数图象的切线斜率,可得倾斜角,从而可得结论.
解答 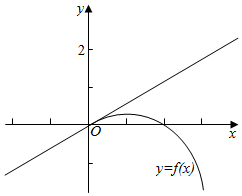 解:由题意,函数图象如图所示,函数在[0,1]上为增函数,在[1,2]上为减函数.
解:由题意,函数图象如图所示,函数在[0,1]上为增函数,在[1,2]上为减函数.
设函数在x=0处,切线斜率为k,则k=f'(0)
∵f'(x)=$\frac{1}{2}$•$\frac{-2(x-1)}{\sqrt{3+2x-{x}^{2}}}$,
∴k=f'(0)=$\frac{\sqrt{3}}{3}$,可得切线的倾斜角为30°,
因此,要使旋转后的图象仍为一个函数的图象,旋转θ后的切线倾斜角最多为90°,也就是说,最大旋转角为90°-30°=60°,即θ的最大值为60°.
故答案为:60°
点评 本题考查了导数的几何意义和函数的图象与图象变化等知识点,将函数图象绕原点逆时针旋转θ后,所得曲线仍是一个函数的图象,求角θ的最大值,属于中档题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
7.已知样本x1,x2,…xm的平均数为$\overline x$,样本y1,y2,…yn的平均数$\overline y$,若样本x1,x2,…xm,y1,y2,…yn的平均数$\overline z$=α$\overline x$+(1-α)$\overline y$,其中0<α≤$\frac{1}{2}$,则m,n的大小关系为( )
| A. | m<n | B. | m>n | C. | m≤n | D. | m≥n |
5.若方程(m-1)x2+(3-m)y2=(m-1)(3-m)表示焦点在y轴上的椭圆,则实数m的取值范围是( )
| A. | (-∞,1) | B. | (1,2) | C. | (2,3) | D. | (3,+∞) |
6.某运动员射击一次所得环数X的分布如下:
现进行两次射击,以该运动员两次射击中最高环数作为他的成绩,记为ξ.
(I)求该运动员两次都命中7环的概率;
(Ⅱ)求ξ的数学期望Eξ.
| X | 0~6 | 7 | 8 | 9 | 10 |
| P | 0 | 0.2 | 0.3 | 0.3 | 0.2 |
(I)求该运动员两次都命中7环的概率;
(Ⅱ)求ξ的数学期望Eξ.
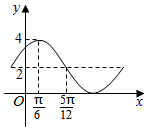 已知函数f(x)=Asin(ωx+φ)+B(A>0,ω,0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(π)的值为3.
已知函数f(x)=Asin(ωx+φ)+B(A>0,ω,0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(π)的值为3.