题目内容
7.用平面区域表示下列不等式组.(1)$\left\{\begin{array}{l}{x≥y}\\{3x+4y-12<0}\end{array}\right.$
(2)$\left\{\begin{array}{l}{x-y+5≥0}\\{x+y+1>0}\\{x≤3}\end{array}\right.$.
分析 由题意,分别画出不等式表示的平面区域,公共部分即为不等式组表示的平面区域.
解答 解:(1)如图 ;
;
(2)不等式组表示的平面区域如图: .
.
点评 本题考查了不等式组表示的平面区域的画法;关键是正确作出每个不等式表示的区域.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
15.给出下列4个命题,其中正确的个数是( )
①若“命题p∧q为真”,则“命题p∨q为真”;
②命题“?x>0,x-lnx>0”的否定是“?x>0,x-lnx≤0”;
②“tanx>0”是“sin2x>0”的充要条件;
④计算:9192除以100的余数是1.
①若“命题p∧q为真”,则“命题p∨q为真”;
②命题“?x>0,x-lnx>0”的否定是“?x>0,x-lnx≤0”;
②“tanx>0”是“sin2x>0”的充要条件;
④计算:9192除以100的余数是1.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
12.在掷均匀硬币的试验中,以下对“大数定理”的理解错误的是( )
| A. | 大量的试验中,出现正面的频率稳定于$\frac{1}{2}$ | |
| B. | 不管试验多少次,出现正面的概率始终为$\frac{1}{2}$ | |
| C. | 试验次数增多,出现正面的经验概率越接近$\frac{1}{2}$ | |
| D. | 试验次数无限增大时,出现正面的频率的极限为$\frac{1}{2}$ |
19.已知|$\overrightarrow{a}$|=8,|$\overrightarrow{b}$|=6,则<$\overrightarrow{a}$,$\overrightarrow{b}$>=150°,则$\overrightarrow{a}$$•\overrightarrow{b}$=( )
| A. | -24 | B. | 24 | C. | -24$\sqrt{3}$ | D. | 24$\sqrt{3}$ |
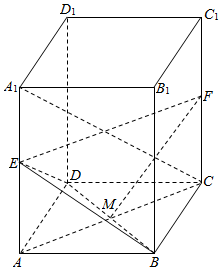 如图正四棱住ABCD-A1B1C1D1中,点E是A1A上的点,M是AC、BD的交点.
如图正四棱住ABCD-A1B1C1D1中,点E是A1A上的点,M是AC、BD的交点.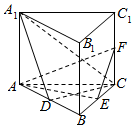 如图,直三棱柱ABC-A1B1C1的底面为正三角形,E、F分别是BC、CC1的中点.
如图,直三棱柱ABC-A1B1C1的底面为正三角形,E、F分别是BC、CC1的中点.