题目内容
5.通过随机询问110名性别不同的大学生是否爱好某项运动,得到如表的列联表:| 男 | 女 | 总计 | |
| 爱好 | 40 | 20 | 60 |
| 不爱好 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |
附临界值表:
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K0 | 0.455 | 0.708 | 1.323 | 2.072 | 3.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | 在犯错误的概率不超过0.5的前提下,认为“爱好该项运动与性别有关” | |
| B. | 在犯错误的概率不超过0.5的前提下,认为“爱好该项运动与性别无关” | |
| C. | 在犯错误的概率不超过0.5%的前提下,认为“爱好该项运动与性别有关” | |
| D. | 在犯错误的概率不超过0.5%的前提下,认为“爱好该项运动与性别无关” |
分析 通过所给的观测值,同临界值表中的数据进行比较,得出9.091>7.879,由此得到结论.
解答 解:由2×2列联表中的数据计算得出K2的观测值k≈9.091,
且9.091>7.879,
所以在犯错误的概率不超过0.5%的前提下,认为“爱好该项运动与性别有关”,
故选:C.
点评 本题考查了独立性检验的应用问题,判断两个变量之间有没有关系,一般需要计算观测值,再用观测值同临界值进行比较,即可得到结论.

练习册系列答案
相关题目
10.已知函数f(x)=(x2-2mx+m2)lnx无极值点,则实数m的取值范围是( )
| A. | (-∞,$-2{e}^{-\frac{3}{2}}$) | B. | (-∞,1] | C. | (-2,0)∪(0,1] | D. | (-∞,$-2{e}^{-\frac{3}{2}}$]∪{1} |
14.欧拉公式eix=cosx+isinx(i为虚数单位)是由瑞士著名数学家欧拉发明的,它将复数、指数函数与三角函数联系起来,将指数函数的定义域扩充为复数,它在复变函数论里占有非常重要的地位,被誉为“数学中的天骄”,根据欧拉公式可知,复数e-2i所对应的点在复平面中位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
12.已知F1、F2是椭圆和双曲线的公共焦点,P是他们的一个公共点,且∠F1PF2=$\frac{π}{3}$,则椭圆和双曲线的离心率之积的最小值为( )
| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 1 |
 均为非零实数,且满足
均为非零实数,且满足 .
. 的值;
的值; 中,若
中,若 ,求
,求 的最大值.
的最大值. B.
B.
 D.2
D.2 的内角
的内角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
, ,已知
,已知 ,
, ,
, ,则
,则 ( )
( ) B.
B. 或
或
 或
或 D.
D.
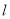 的参数方程式
的参数方程式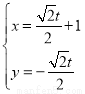 (
(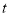 是参数).以坐标原点为极点,
是参数).以坐标原点为极点,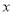 轴的正半轴为极轴,且取相同的长度单位建立极坐标系,圆
轴的正半轴为极轴,且取相同的长度单位建立极坐标系,圆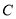 的极坐标方程为
的极坐标方程为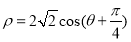 .
.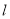 的普通方程与圆
的普通方程与圆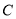 的直角坐标方程;
的直角坐标方程;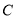 与直线
与直线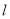 交于
交于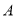 、
、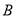 两点,若
两点,若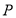 点的直角坐标为
点的直角坐标为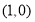 ,求
,求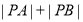 的值.
的值.