题目内容
17.若sinθ+cosθ=$\frac{1}{3}$,则sinθcosθ=$-\frac{4}{9}$.分析 由(sinθ+cosθ)2=$\frac{1}{9}$,打开,根据同角三角函数基本关系式,可得答案.
解答 解:∵sinθ+cosθ=$\frac{1}{3}$,
∴(sinθ+cosθ)2=$\frac{1}{9}$,
∴1+2sinθcosθ=$\frac{1}{9}$.
则sinθcosθ=$-\frac{4}{9}$.
故答案为$-\frac{4}{9}$
点评 本题考查了同角三角函数基本关系式,考查了计算能力,属于基础题.

练习册系列答案
相关题目
5.通过随机询问110名性别不同的大学生是否爱好某项运动,得到如表的列联表:
由K2=$\frac{n(ad-bc)^{2}}{(a+b)(b+c)(a+c)(b+d)}$,算得其观测值k≈9.091.
附临界值表:
参照附表,得到的正确结论是( )
| 男 | 女 | 总计 | |
| 爱好 | 40 | 20 | 60 |
| 不爱好 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |
附临界值表:
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K0 | 0.455 | 0.708 | 1.323 | 2.072 | 3.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | 在犯错误的概率不超过0.5的前提下,认为“爱好该项运动与性别有关” | |
| B. | 在犯错误的概率不超过0.5的前提下,认为“爱好该项运动与性别无关” | |
| C. | 在犯错误的概率不超过0.5%的前提下,认为“爱好该项运动与性别有关” | |
| D. | 在犯错误的概率不超过0.5%的前提下,认为“爱好该项运动与性别无关” |
 ,则下列不等式错误的是( )
,则下列不等式错误的是( ) B.
B.
 D.
D.
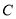 :
: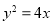 的焦点为
的焦点为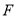 ,定点
,定点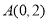 ,若射线
,若射线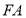 与抛物线
与抛物线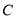 交于点
交于点 ,与抛物线
,与抛物线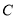 的准线交于点
的准线交于点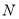 ,则
,则 的值是( )
的值是( )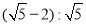 B.
B.
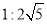 D.
D.