题目内容
10.已知函数f(x)=(x2-2mx+m2)lnx无极值点,则实数m的取值范围是( )| A. | (-∞,$-2{e}^{-\frac{3}{2}}$) | B. | (-∞,1] | C. | (-2,0)∪(0,1] | D. | (-∞,$-2{e}^{-\frac{3}{2}}$]∪{1} |
分析 函数f(x)=(x2-2mx+m2)lnx(x>0),f′(x)=(2x-2m)lnx+(x-2m+$\frac{{m}^{2}}{x}$)=$\frac{x-m}{x}$(2xlnx+x-m).当x>1且x>m时,即x>max(1,m)时,f′(x)>0,可得函数f(x)单调递增,满足函数f(x)取极值.对m分类讨论,利用导数研究函数的单调性极值即可得出.
解答 解:函数f(x)=(x2-2mx+m2)lnx(x>0),f′(x)=(2x-2m)lnx+(x-2m+$\frac{{m}^{2}}{x}$)=$\frac{x-m}{x}$(2xlnx+x-m).
当x>1且x>m时,即x>max(1,m)时,f′(x)>0,∴函数f(x)单调递增,满足函数f(x)无极值.
①m>1时,只要求x∈(0,m)时,f′(x)≥0即可,只需2xlnx+2x-m≤0即可.∴m≥2x+2xlnx,
令g(x)=x+2xlnx,g′(x)=3+2lnx,可得函数g(x)的图象: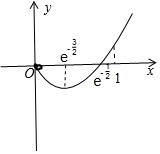
∴m>g(m)=m+2mlnm,解得:m<1,舍去.
②m=1时,只要求x∈(0,1)时,f′(x)≥0即可,即1≥g(x).
而g(x)max=g(1)=1,成立,即m=1满足条件.
③当0<m<1时,只要求x∈(0,1)时,f′(x)≥0即可,∴m≥g(x)max=g(1)=1,不符合题意,舍去.
④当m≤0时,只要求x∈(0,1)时,f′(x)≥0即可,∴m≤g(x)min=$g({e}^{-\frac{3}{2}})$=-2${e}^{-\frac{3}{2}}$,即m≤-2${e}^{-\frac{3}{2}}$.
综上可得:m的取值范围是$(-∞,-2{e}^{-\frac{3}{2}}]$∪{1}.
故选:D.
点评 本题考查了利用导数研究函数的单调性极值、分类讨论思想方法,考查了推理能力与计算能力,属于难题.

| 男 | 女 | 总计 | |
| 爱好 | 40 | 20 | 60 |
| 不爱好 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |
附临界值表:
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K0 | 0.455 | 0.708 | 1.323 | 2.072 | 3.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | 在犯错误的概率不超过0.5的前提下,认为“爱好该项运动与性别有关” | |
| B. | 在犯错误的概率不超过0.5的前提下,认为“爱好该项运动与性别无关” | |
| C. | 在犯错误的概率不超过0.5%的前提下,认为“爱好该项运动与性别有关” | |
| D. | 在犯错误的概率不超过0.5%的前提下,认为“爱好该项运动与性别无关” |
 上的不间断函数
上的不间断函数 满足:①当
满足:①当 时,
时, 恒成立;②对任意的
恒成立;②对任意的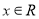 都有
都有 .又函数
.又函数 满足:对任意的
满足:对任意的 ,都有
,都有 成立,当
成立,当 时,
时, .若关于
.若关于 的不等式
的不等式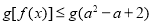 ,对于
,对于 恒成立,则
恒成立,则 的取值范围为____________.
的取值范围为____________.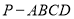 中,底面
中,底面 为菱形,
为菱形, 为
为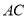 与
与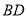 的交点,
的交点,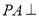 平面
平面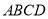 ,
,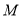 为
为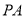 中点,
中点,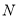 为
为 中点.
中点.
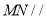 平面
平面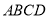 ;
;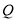 为
为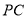 中点,
中点,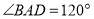 ,
,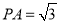 ,
,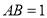 ,求三棱锥
,求三棱锥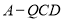 的体积.
的体积. ,集合
,集合 ,
, ,则
,则 ( )
( ) B.
B.
 D.
D.
 秦九韶是我国南宋时期的数学家,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入n,x的值分别为3,3,则输出v的值为48.
秦九韶是我国南宋时期的数学家,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入n,x的值分别为3,3,则输出v的值为48.