题目内容
方程2sin(x+
)+2a-1=0在[0,π]上有两个不等的实根,则实数a的取值范围是 .
| π | 3 |
分析:令y1(x)=2sin(x+
),y2(x)=1-2a,依题意,在同一坐标系中作出两函数的图象,利用正弦函数的单调性即可求得实数a的取值范围.
| π |
| 3 |
解答:解:∵1-2a=2sin(x+
),
令y1(x)=2sin(x+
),y2(x)=1-2a,
∵x∈[0,π],
∴x+
∈[
,
],
方程2sin(x+
)+2a-1=0在[0,π]上有两个不等的实根,
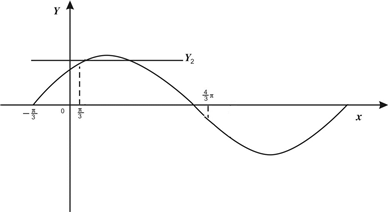
由图知,
≤2sin(x+
)<2,即
≤1-2a<2,
∴-2<2a-1≤-
,
解得-
<a≤
.
∴实数a的取值范围是(-
,
].
故答案为:(-
,
].
| π |
| 3 |
令y1(x)=2sin(x+
| π |
| 3 |
∵x∈[0,π],
∴x+
| π |
| 3 |
| π |
| 3 |
| 4π |
| 3 |
方程2sin(x+
| π |
| 3 |

由图知,
| 3 |
| π |
| 3 |
| 3 |
∴-2<2a-1≤-
| 3 |
解得-
| 1 |
| 2 |
1-
| ||
| 2 |
∴实数a的取值范围是(-
| 1 |
| 2 |
1-
| ||
| 2 |
故答案为:(-
| 1 |
| 2 |
1-
| ||
| 2 |
点评:本题考查直线与正弦曲线的位置关系,着重考查正弦函数的图象与单调性质,考查综合分析与运算能力,属于中档题.

练习册系列答案
相关题目
设x∈(0,π),关于x的方程2Sin(x+
)=a有2个不同的实数解,则实数a的取值范围是( )
| π |
| 3 |
A、(-
| ||||
B、(-
| ||||
C、(
| ||||
D、(-2,
|