题目内容
17. 如图,直三棱柱ABC-A1B1C1中,AC=BC=$\frac{1}{2}$AA1=1,D是棱AA1的中点,DC1⊥BD.
如图,直三棱柱ABC-A1B1C1中,AC=BC=$\frac{1}{2}$AA1=1,D是棱AA1的中点,DC1⊥BD.(1)证明:DC1⊥BC;
(2)若∠ACB=90°,求点C到平面BDC1的距离.
分析 (1)证明DC1⊥面BCD,即可证明DC1⊥BC;
(2)过C作CE⊥BD,则CE⊥面BC1D,CE为点C到平面BDC1的距离,利用等面积求点C到平面BDC1的距离.
解答 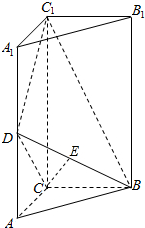 (1)证明:在Rt△DAC中,AD=AC,∴∠ADC=45°
(1)证明:在Rt△DAC中,AD=AC,∴∠ADC=45°
同理:∠A1DC1=45°,∴∠CDC1=90°
∴DC1⊥DC,DC1⊥BD
∵DC∩BD=D
∴DC1⊥面BCD
∵BC?面BCD
∴DC1⊥BC;
(2)解:∵DC1⊥面BCD,DC1?面BC1D
∴面BC1D⊥面BCD,
过C作CE⊥BD,则CE⊥面BC1D,CE为点C到平面BDC1的距离.
△BCD中,BC=1,CD=$\sqrt{2}$,BD=$\sqrt{3}$,BC⊥CD,S△BCD=$\frac{\sqrt{2}}{2}$,
∴$\frac{1}{2}×\sqrt{3}h$=$\frac{\sqrt{2}}{2}$,
∴h=$\frac{\sqrt{6}}{3}$.
点评 本题考查线面垂直的判定与性质,考查点到平面距离的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
12.已知抛物线y2=4x的准线l与双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)相切,且l与该双曲线的渐近线相交于A、B两点,若△ABO(O为原点)为钝角三角形,则双曲线的离心率的取值范围为( )
| A. | ($\sqrt{3}$,+∞) | B. | (1,$\sqrt{3}$) | C. | (1,$\sqrt{2}$) | D. | ($\sqrt{2}$,+∞) |
2.盒子中装有5个零件,其中有2个次品,现从中随机抽取2个,则恰有一个次品的概率为( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
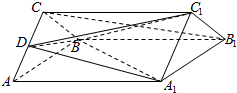 如图,在三棱柱ABC-A1B1C1中,棱AC的中点为D
如图,在三棱柱ABC-A1B1C1中,棱AC的中点为D 如图,已知椭圆C的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的两条渐近线为l1、l2.过椭圆C的右焦点F作直线l,使l丄l1.设直线l与椭圆C的两个交点由上至下依次为A,B,直线l与直线l2交于P点.
如图,已知椭圆C的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的两条渐近线为l1、l2.过椭圆C的右焦点F作直线l,使l丄l1.设直线l与椭圆C的两个交点由上至下依次为A,B,直线l与直线l2交于P点.