题目内容
在△ABC中,记∠BAC=x(角的单位是弧度制),△ABC的面积为S,且 .
.(1)求x的取值范围;
(2)就(1)中x的取值范围,求函数
 的最大值、最小值.
的最大值、最小值.
【答案】分析:(1)利用三角形面积公式,退席已知中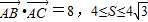 ,我们易确定tanx的范围,结合x为三角形的内角,我们易求出x的取值范围;
,我们易确定tanx的范围,结合x为三角形的内角,我们易求出x的取值范围;
(2)结合(1)的结论,利用降幂公式和辅助角公式,我们易将函数的解析式化为正弦型函数的形式,进而根据正弦型函数的性质即可得到答案.
解答:解:(1)∵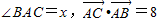 ,
,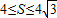 ,
,
又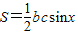 ,
,
∴bccosx=8,S=4tanx,即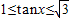 .(4分)
.(4分)
∴所求的x的取值范围是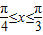 .(7分)
.(7分)
(2)∵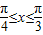 ,
,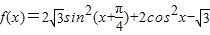
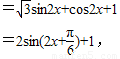 (9分)
(9分)
∴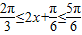 ,
,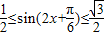 .(11分)
.(11分)
∴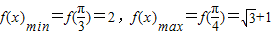 .(14分)
.(14分)
点评:本题考查的知识点是三角函数的最值,平面向量数量积的含义与物理意义,其中根据平面向量数理积的含义及三角形面积结合正切函数的性质,求出X的取值范围是解答本题的关键.
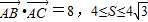 ,我们易确定tanx的范围,结合x为三角形的内角,我们易求出x的取值范围;
,我们易确定tanx的范围,结合x为三角形的内角,我们易求出x的取值范围;(2)结合(1)的结论,利用降幂公式和辅助角公式,我们易将函数的解析式化为正弦型函数的形式,进而根据正弦型函数的性质即可得到答案.
解答:解:(1)∵
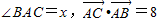 ,
,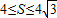 ,
,又
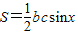 ,
,∴bccosx=8,S=4tanx,即
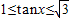 .(4分)
.(4分)∴所求的x的取值范围是
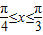 .(7分)
.(7分)(2)∵
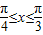 ,
,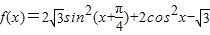
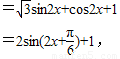 (9分)
(9分)∴
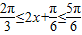 ,
,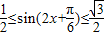 .(11分)
.(11分)∴
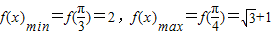 .(14分)
.(14分)点评:本题考查的知识点是三角函数的最值,平面向量数量积的含义与物理意义,其中根据平面向量数理积的含义及三角形面积结合正切函数的性质,求出X的取值范围是解答本题的关键.

练习册系列答案
相关题目
 (2013•湖北)如图,某地质队自水平地面A,B,C三处垂直向地下钻探,自A点向下钻到A1处发现矿藏,再继续下钻到A2处后下面已无矿,从而得到在A处正下方的矿层厚度为A1A2=d1.同样可得在B,C处正下方的矿层厚度分别为B1B2=d2,C1C2=d3,且d1<d2<d3.过AB,AC的中点M,N且与直线AA2平行的平面截多面体A1B1C1-A2B2C2所得的截面DEFG为该多面体的一个中截面,其面积记为S中.
(2013•湖北)如图,某地质队自水平地面A,B,C三处垂直向地下钻探,自A点向下钻到A1处发现矿藏,再继续下钻到A2处后下面已无矿,从而得到在A处正下方的矿层厚度为A1A2=d1.同样可得在B,C处正下方的矿层厚度分别为B1B2=d2,C1C2=d3,且d1<d2<d3.过AB,AC的中点M,N且与直线AA2平行的平面截多面体A1B1C1-A2B2C2所得的截面DEFG为该多面体的一个中截面,其面积记为S中.