题目内容
在△ABC中，记BC=a，CA=b，AB=c，若9a2+9b2-19c2=0，求
的值．
| cotC | cotA+cotB |
分析：可将9a2+9b2-19c2=0，转化为9（a2+b2-c2）=10c2，逆用余弦定理得到18abcosC=10c2，再利用正弦定理转化为9sinAsinBcosC=5sin2C，再将
中的切化弦，逆用两角和的正弦公式，最后代入即可．
| cotC |
| cotA+cotB |
解答：解：∵9（a2+b2-c2）=10c2，由余弦定理a2+b2-c2=2abcosC得：
18abcosC=10c2，又
=
=
=2R，
∴9sinAsinBcosC=5sin2C，
∴
=
=
=
=
=
．
18abcosC=10c2，又
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
∴9sinAsinBcosC=5sin2C，
∴
| cotC |
| cotA+cotB |
| ||||
|
=
| sinAsinBcosC |
| sinC(cosAsinB+sinAcosB) |
=
| sinAsinBcosC |
| sinCsin(A+B) |
=
| sinAsinBcosC |
| sin2C |
| 5 |
| 9 |
点评：本题考查余弦定理与正弦定理，着重考查整体代入与转化的思想，属于中档题．
练习册系列答案
相关题目
（2013•湖北）如图，某地质队自水平地面A，B，C三处垂直向地下钻探，自A点向下钻到A1处发现矿藏，再继续下钻到A2处后下面已无矿，从而得到在A处正下方的矿层厚度为A1A2=d1．同样可得在B，C处正下方的矿层厚度分别为B1B2=d2，C1C2=d3，且d1＜d2＜d3．过AB，AC的中点M，N且与直线AA2平行的平面截多面体A1B1C1-A2B2C2所得的截面DEFG为该多面体的一个中截面，其面积记为S中．
＝__________．
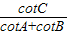的值．