题目内容
在△ABC中，记向量
=
+
，
=
+
，且∠A=120°，则
，
的夹角为（ ）
| m |
| ||
|
|
| ||
|
|
| n |
| ||
|
|
| ||
|
|
| m |
| n |
分析：特殊值法，令B=C=30°，2求出
•
和|
|、|
|，根据向量的数量积求向量的夹角公式，代入即可求得结果．
| m |
| n |
| m |
| n |
解答：解：令B=C=30°，
•
=(
+
)•(
+
)
=
•
+
•
+
•
+
•
=
-
-
-
=2-
=
．
|
|2=(
+
)2=
+
+2
•
=4+
-4
=
，
|
|2=4+
-4
=
，
∴|
|||
|=
，
cos＜
，
＞=
，
∴
，
的夹角60°．
故选B．
| m |
| n |
| ||
|
|
| ||
|
|
| ||
|
|
| ||
|
|
=
| ||
|
|
| ||
|
|
| ||
|
|
| ||
|
|
| ||
|
|
| ||
|
|
| ||
|
|
| ||
|
|
=
| 1 |
| cosA |
| 1 |
| cosA |
| 1 |
| cosA |
| 1 |
| cosCcosB |
| 1 |
| cosCcosB |
| 2 |
| 3 |
|
| m |
| ||
|
|
| ||
|
|
| 1 |
| (cosA)2 |
| 1 |
| (cosC)2 |
| ||
|
|
| ||
|
|
=4+
| 1 |
| (cosC)2 |
| cosB |
| cosC |
| 4 |
| 3 |
|
| n |
| 1 |
| (cosB)2 |
| cosC |
| cosB |
| 4 |
| 3 |
∴|
| m |
| n |
| 4 |
| 3 |
cos＜
| m |
| n |
| 1 |
| 2 |
∴
| m |
| n |
故选B．
点评：此题是个基础题．考查数量积表示两个向量的夹角，以及灵活应用知识分析解决问题的能力和计算能力．
练习册系列答案
相关题目
，且∠A=120°，则
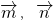的夹角为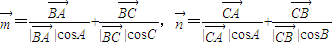
，且∠A=120°，则
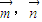的夹角为（ ）