题目内容
3.设命题p:?x>0,lnx>lgx,命题q:?x>0,$\sqrt{x}$=1-x2,则下列命题为真命题的是( )| A. | p∧q | B. | ¬p∧¬q | C. | p∧¬q | D. | ¬p∧q |
分析 命题p:是假命题,例如取x=1,则lnx=lgx=0.命题q:画出图象:即可判断出结论.
解答  解:命题p:?x>0,lnx>lgx,是假命题,例如取x=1,则lnx=lgx=0.
解:命题p:?x>0,lnx>lgx,是假命题,例如取x=1,则lnx=lgx=0.
命题q:?x>0,$\sqrt{x}$=1-x2,画出图象可知:q为真命题.
则下列命题为真命题的是¬p∧q.
故选:D.
点评 本题考查了函数的性质、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
13.已知平面向量$\overrightarrow{a}$=(-$\sqrt{3}$,m),$\overrightarrow{b}$=(2,1)且$\overrightarrow{a}$⊥$\overrightarrow{b}$,则实数m的值为( )
| A. | $-2\sqrt{3}$ | B. | $2\sqrt{3}$ | C. | $4\sqrt{3}$ | D. | $6\sqrt{3}$ |
14.已知数列{an}满足2Sn=4an-1.则log2a3与log2a9的等差中项为( )
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
18.已知函数f(x)=sin(2ωx+$\frac{π}{3}$)(ω>0)下的最小正周期为π,则函数的图象( )
| A. | 关于直线x=$\frac{13π}{12}$对称 | B. | 关于点(-$\frac{π}{12}$,0)对称 | ||
| C. | 关于直线x=-$\frac{7π}{12}$对称 | D. | 关于点($\frac{π}{4}$,0)对称 |
8.函数f(x)=2sin(ωx+φ)(w>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(0)+f($\frac{17π}{12}$)的值为( )
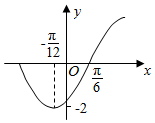
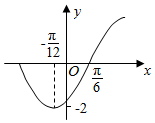
| A. | 2-$\sqrt{3}$ | B. | 2+$\sqrt{3}$ | C. | 1-$\frac{\sqrt{3}}{2}$ | D. | 1+$\frac{\sqrt{3}}{2}$ |
12.已知集合A={x|x2<1},B={x|log2x<1},则A∩B=( )
| A. | {x|-1<x<1} | B. | {x|0<x<1} | C. | {x|0<x<2} | D. | {x|-1<x<2} |
13.已知集合A={x|lnx<1},B={x|0<x<C},若A∪B=B,则C的取值范围是( )
| A. | (0,1] | B. | [1,+∞) | C. | (0,e] | D. | [e,+∞) |
 如图,已知正三棱柱ABC-A1B1C1的体积为$9\sqrt{3}$,底面边长为3,求异面直线BC1与AC所成的角的大小.
如图,已知正三棱柱ABC-A1B1C1的体积为$9\sqrt{3}$,底面边长为3,求异面直线BC1与AC所成的角的大小.