题目内容
14.已知数列{an}满足2Sn=4an-1.则log2a3与log2a9的等差中项为( )| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
分析 由已知条件可判数列为等比数列,可得通项公式,进而可得log2a3与log2a9的值,可得其等差中项.
解答 解:∵2Sn=4an-1,∴当n≥2时2Sn-1=4an-1-1,
两式相减可得2Sn-2Sn-1=4an-1-(4an-1-1),
∴2an=4an-4an-1,∴an=2an-1,
由当n=1时,2S1=4a1-1即2a1=4a1-1,解得a1=$\frac{1}{2}$,
∴数列{an}时首项为$\frac{1}{2}$公比为2的等比数列,
∴an=$\frac{1}{2}$×2n-1=2n-2,
∴log2a3=1,log2a9=7,
∴等差中项为4
故选:B
点评 本题考查等差数列和等比数列,涉及等比数列的判定,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.图1是某学习小组学生数学考试成绩的茎叶图,1号到16号的同学的成绩依次为A1,A2,…,A11,图2是统计茎叶图中成绩在一定范围内的学生情况的程序框图,那么该程序框图输出的结果是( )
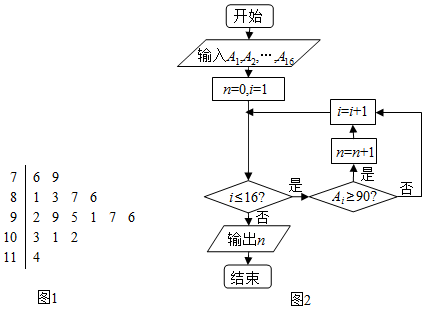

| A. | 6 | B. | 10 | C. | 7 | D. | 16 |
6.△ABC中,$|{\overrightarrow{AB}}|=\sqrt{3}$,$|{\overrightarrow{AC}}|=1$,D是BC边中垂线上任意一点,则$\overrightarrow{AD}•\overrightarrow{CB}$的值是( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | -1 |
3.设命题p:?x>0,lnx>lgx,命题q:?x>0,$\sqrt{x}$=1-x2,则下列命题为真命题的是( )
| A. | p∧q | B. | ¬p∧¬q | C. | p∧¬q | D. | ¬p∧q |
 在如图所示的直三棱柱ABC-A1B1C1,AC=1,BC=$\sqrt{2}$,AB=$\sqrt{3}$,侧棱AA1=1,点D,M分别为A1B,B1C1的中点.
在如图所示的直三棱柱ABC-A1B1C1,AC=1,BC=$\sqrt{2}$,AB=$\sqrt{3}$,侧棱AA1=1,点D,M分别为A1B,B1C1的中点.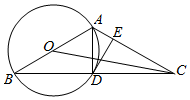 如图,以△ABC的边AB为直径作⊙O,⊙O与边BC的交点D恰为BC边的中点,过点D作DE⊥AC于点E.
如图,以△ABC的边AB为直径作⊙O,⊙O与边BC的交点D恰为BC边的中点,过点D作DE⊥AC于点E.