题目内容
15.已知直线$l:\frac{x}{a}+\frac{y}{b}=1({a>0,b>0})$过点A(1,2),则a+8b的最小值为25.分析 由题意知$\frac{1}{a}$+$\frac{2}{b}$=1,从而化简a+8b=8$\frac{b}{a}$+2$\frac{a}{b}$+17,从而利用基本不等式求解.
解答 解:由题意知,
$\frac{1}{a}$+$\frac{2}{b}$=1,
故a+8b=(a+8b)($\frac{1}{a}$+$\frac{2}{b}$)
=8$\frac{b}{a}$+2$\frac{a}{b}$+17
≥2$\sqrt{16}$+17=25,
(当且仅当8$\frac{b}{a}$=2$\frac{a}{b}$,a=2b时,等号成立),
故答案为:25.
点评 本题考查了基本不等式的应用及直线方程的应用.

练习册系列答案
相关题目
5.图1是某学习小组学生数学考试成绩的茎叶图,1号到16号的同学的成绩依次为A1,A2,…,A11,图2是统计茎叶图中成绩在一定范围内的学生情况的程序框图,那么该程序框图输出的结果是( )
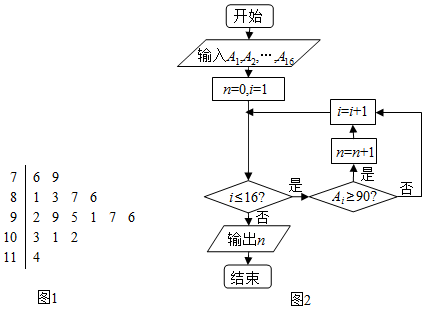

| A. | 6 | B. | 10 | C. | 7 | D. | 16 |
6.△ABC中,$|{\overrightarrow{AB}}|=\sqrt{3}$,$|{\overrightarrow{AC}}|=1$,D是BC边中垂线上任意一点,则$\overrightarrow{AD}•\overrightarrow{CB}$的值是( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | -1 |
3.设命题p:?x>0,lnx>lgx,命题q:?x>0,$\sqrt{x}$=1-x2,则下列命题为真命题的是( )
| A. | p∧q | B. | ¬p∧¬q | C. | p∧¬q | D. | ¬p∧q |
20.在斜△ABC中,内角A,B,C所对的边长分别是a,b,c,asinB+bcos(B+C)=0,sinA+sin(B-C)=2$\sqrt{2}$sin2C,且△ABC的面积为1,则a的值为( )
| A. | 2 | B. | $\sqrt{5}$ | C. | $\sqrt{6}$ | D. | $\sqrt{7}$ |