题目内容
6.直线$\left\{\begin{array}{l}{x=1+t}\\{y=1-t}\end{array}\right.$(t为参数)的倾斜角的大小为$\frac{3π}{4}$.分析 化参数方程为普通方程,求出斜率,即可求得倾斜角.
解答 解:$\left\{\begin{array}{l}{x=1+t}\\{y=1-t}\end{array}\right.$(t为参数)化参数方程为普通方程,两方程相加可得x+y=2,
则直线的斜率为-1,
故倾斜角为$\frac{3π}{4}$.
故答案为:$\frac{3π}{4}$.
点评 本题考查直线的斜率与倾斜角的关系,解题的关键是化参数方程为普通方程,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.下列函数中,在区间(0,2)上为增函数的是( )
| A. | y=-2x+1 | B. | y=$\frac{1}{3}$x2+1 | C. | y=-x2-x-1 | D. | y=x2-x+1 |
11.${∫}_{-1}^{1}$x2dx=( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
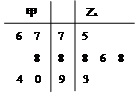 甲乙两位歌手在“中国好声音”选拔赛中,5次得分情况如茎叶图所示,
甲乙两位歌手在“中国好声音”选拔赛中,5次得分情况如茎叶图所示,