题目内容
下列说法正确的是( )
| A、一个命题的逆命题为真,则它的逆否命题一定为真 |
| B、若a+b>3,则a>1或b>2 |
| C、命题“所有的矩形都是正方形”的否命题和命题的否定均为真命题 |
| D、“a2+b2=0,则a,b全为0”的逆否命题是“若a,b全不为0,则a2+b2≠0” |
考点:命题的真假判断与应用
专题:简易逻辑
分析:A.一个命题的逆命题与它的逆否命题,二者之间的真假不存在必然的关系;
B.若a+b>3,则a>1或b>2,不正确,
C.命题“所有的矩形都是正方形”的否命题为“不是矩形的四边形不是正方形”,
命题的否定为“至少存在一个矩形不是正方形”,即可判断出;
D.“a2+b2=0,则a,b全为0”的逆否命题是“若a,b不全为0,则a2+b2≠0”,“a,b不全为0”与“a,b全不为0”二者意义不同.
B.若a+b>3,则a>1或b>2,不正确,
C.命题“所有的矩形都是正方形”的否命题为“不是矩形的四边形不是正方形”,
命题的否定为“至少存在一个矩形不是正方形”,即可判断出;
D.“a2+b2=0,则a,b全为0”的逆否命题是“若a,b不全为0,则a2+b2≠0”,“a,b不全为0”与“a,b全不为0”二者意义不同.
解答:
解:A.一个命题的逆命题为真,则它的逆否命题不一定为真,二者之间真假不存在必然的关系,因此不正确;
B.若a+b>3,则a>1或b>2,不正确,
C.命题“所有的矩形都是正方形”的否命题为“不是矩形的四边形不是正方形”,
命题的否定为“至少存在一个矩形不是正方形”,均为真命题.因此C正确
D.“a2+b2=0,则a,b全为0”的逆否命题是“若a,b不全为0,则a2+b2≠0”,因此D不正确.
故选:C.
B.若a+b>3,则a>1或b>2,不正确,
C.命题“所有的矩形都是正方形”的否命题为“不是矩形的四边形不是正方形”,
命题的否定为“至少存在一个矩形不是正方形”,均为真命题.因此C正确
D.“a2+b2=0,则a,b全为0”的逆否命题是“若a,b不全为0,则a2+b2≠0”,因此D不正确.
故选:C.
点评:本题综合考查了四种命题之间的关系、命题的否定等基础知识,注意一些词语的否定,属于中档题.

练习册系列答案
相关题目
 按照如图的程序框图执行,若输出结果为31,则M处的条件为( )
按照如图的程序框图执行,若输出结果为31,则M处的条件为( )| A、k≥32 | B、k<16 |
| C、k<32 | D、k≥16 |
二项式(
-
)n的展开式中第4项为常数项,则常数项为( )
| x |
| 1 | |||
|
| A、10 | B、-10 |
| C、20 | D、-20 |
设z=
,若复数z为纯虚数(其中i是虚数单位),则实数a等于( )
| 1-ai |
| i |
| A、-1 | ||
| B、0 | ||
| C、1 | ||
D、
|
 甲、乙两个学习小组各有10名同学,他们在一次数学测验中成绩的茎叶图(如图),则他们在这次测验中成绩较好的是
甲、乙两个学习小组各有10名同学,他们在一次数学测验中成绩的茎叶图(如图),则他们在这次测验中成绩较好的是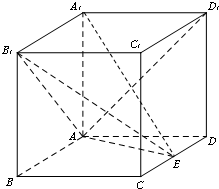 在长方体ABCD-A1B1C1D1中,AA1=AD=1,E为线段CD中点.
在长方体ABCD-A1B1C1D1中,AA1=AD=1,E为线段CD中点.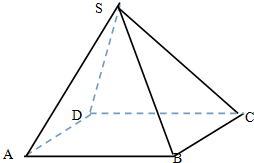 如图四棱锥S-ABCD中,底面是边长为2厘米的正方形,侧棱长都是2厘米.
如图四棱锥S-ABCD中,底面是边长为2厘米的正方形,侧棱长都是2厘米.