题目内容
函数f(x)=
|x-i|的最小值为 .
| 19 |
 |
| i=1 |
考点:绝对值三角不等式,函数的最值及其几何意义
专题:计算题,不等式的解法及应用
分析:利用绝对值的不等式的性质求解即可.
解答:
解:|x-1|+|x-19|≥18,当1≤x≤19时取等号;
|x-2|+|x-18|≥16,当2≤x≤18时取等号;
|x-3|+|x-17|≥14,当3≤x≤17时取等号;
…
|x-9|+|x-11|≥2,当9≤x≤11时取等号;
|x-10|≥0,当x=10时取等号;
将上述所有不等式累加得|x-1|+|x-2|+|x-3|+…+|x-19|≥18+16+14+…+2+0=90(当且仅当x=10时取得最小值)
故答案为:90.
|x-2|+|x-18|≥16,当2≤x≤18时取等号;
|x-3|+|x-17|≥14,当3≤x≤17时取等号;
…
|x-9|+|x-11|≥2,当9≤x≤11时取等号;
|x-10|≥0,当x=10时取等号;
将上述所有不等式累加得|x-1|+|x-2|+|x-3|+…+|x-19|≥18+16+14+…+2+0=90(当且仅当x=10时取得最小值)
故答案为:90.
点评:本题主要考查求和符号的意义和绝对值的不等式的性质,难度较大.

练习册系列答案
相关题目
函数y=log
(x2-3x+2)的单调递增区间为( )
| 1 |
| 2 |
| A、(-∞,1) | ||
B、(-∞,
| ||
C、[
| ||
| D、(2,+∞) |
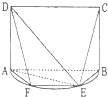 如图,E是以AB为直径的半圆O上异于点A,B的点,边长为4的正方形ABCD所在的平面垂直于该半圆所在的平面.
如图,E是以AB为直径的半圆O上异于点A,B的点,边长为4的正方形ABCD所在的平面垂直于该半圆所在的平面.