题目内容
下列说法正确的是 .
①6名学生争夺3项冠军,冠军的获得情况共有36种.
②设a,b∈R,“a=0”是“复数a+bi是纯虚数”的必要不充分条件.
③(2+3x)10的展开式中含有x8的项的系数与该项的二项式系数相同.
①6名学生争夺3项冠军,冠军的获得情况共有36种.
②设a,b∈R,“a=0”是“复数a+bi是纯虚数”的必要不充分条件.
③(2+3x)10的展开式中含有x8的项的系数与该项的二项式系数相同.
考点:命题的真假判断与应用
专题:简易逻辑,排列组合,二项式定理
分析:①每一项冠军的情况都有6种,故6名学生争夺三项冠军,获得冠军的可能的种数是 63,即可判断;
②当a=0,b≠0,复数a+bi为纯虚数,再由充分必要条件的定义,即可判断;
③由二项式的展开式的通项,写出x8的项的系数与该项的二项式系数,即可判断.
②当a=0,b≠0,复数a+bi为纯虚数,再由充分必要条件的定义,即可判断;
③由二项式的展开式的通项,写出x8的项的系数与该项的二项式系数,即可判断.
解答:
解:①每一项冠军的情况都有6种,故6名学生争夺三项冠军,获得冠军的可能的种数是 63=216种,故①错;
②设a,b∈R,“复数a+bi是纯虚数”可推出“a=0”,反之成立,故②正确;
③(2+3x)10的展开式中含有x8的项的系数为
•4•38,二项式系数为
,故不同,即③错.
故答案为:②
②设a,b∈R,“复数a+bi是纯虚数”可推出“a=0”,反之成立,故②正确;
③(2+3x)10的展开式中含有x8的项的系数为
| C | 8 10 |
| C | 8 10 |
故答案为:②
点评:本题主要考查排列组合、二项式定理和充分必要条件的判断,是一道基础题.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
已知复数z满足
=1-2i,则z=( )
| z |
| 1+2i |
| A、-5 | B、5 | C、-3 | D、3 |
已知不等式
<0的解集为P,若x0∈P,则“|x0|<1“的概率为( )
| x-5 |
| x+1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
设
=(sin25°,cos25°),
=(cos25°,sin25°),则
与
的夹角是( )
| a |
| b |
| a |
| b |
| A、50° | B、40° |
| C、90° | D、0° |

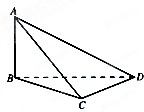 如图,已知AB⊥平面BCD,BC⊥CD,则该三棱锥中互相垂直的平面有
如图,已知AB⊥平面BCD,BC⊥CD,则该三棱锥中互相垂直的平面有