题目内容
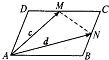
(1)如图,平行四边形ABCD中,M、N分别为DC、BC的中点,已知
=
、
=
,试用
、
表示
和
.
(2)在△ABC中,若
=
,
=
若P,Q,S为线段BC的四等分点,试证:
+
+
=
(
+
);
| AM |
| c |
| AN |
| d |
| c |
| d |
| AB |
| AD |
(2)在△ABC中,若
| AB |
| a |
| AC |
| b |
| AP |
| AQ |
| AS |
| 3 |
| 2 |
| a |
| b |

(1)由
=
,
=
∴
=
+
,
=
+
即
解得:
=
-
=
-
(7分)
(2)证明:
=
+
,
=
+
,
=
+
∴
+
+
=
(
+
),
∴
+
+
=
(
+
)(14分)
| DM |
| 1 |
| 2 |
| AB |
| BN |
| 1 |
| 2 |
| AD |
∴
| c |
| AD |
| DM |
| d |
| AB |
| BN |
即
|
解得:
| AB |
| 4 |
| 3 |
| d |
| 2 |
| 3 |
| c |
| AD |
| 4 |
| 3 |
| c |
| 2 |
| 3 |
| d |
(2)证明:
| AP |
| 3 |
| 4 |
| AB |
| 1 |
| 4 |
| AC |
| AQ |
| 1 |
| 2 |
| AB |
| 1 |
| 2 |
| AC |
| AC |
| 1 |
| 4 |
| AB |
| 3 |
| 4 |
| AC |
∴
| AP |
| AQ |
| AC |
| 3 |
| 2 |
| AB |
| AC |
∴
| AP |
| AQ |
| AC |
| 3 |
| 2 |
| a |
| b |

练习册系列答案
相关题目
 =m
=m +n
+n ,且m+n=1.
,且m+n=1. ,
,  =
=
 +
+
 ,则△ABP的面积与△ABQ的面积之比为( )
,则△ABP的面积与△ABQ的面积之比为( )





 ,则
,则 ;②若
;②若 ,使
,使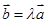 ;
; 是非零向量,
是非零向量, ,那么
,那么 ;④平面内任意两个非零向量都可以作为表示平面内任意一个向量的一组基底。其中正确结论的个数是( )
;④平面内任意两个非零向量都可以作为表示平面内任意一个向量的一组基底。其中正确结论的个数是( )



 =λ
=λ +μ
+μ ,则λμ的最大值为( )
,则λμ的最大值为( )

