题目内容
已知四面体OABC中,OA、OB、OC两两相互垂直, ,
, ,D为四面体OABC外一点.给出下列命题:①不存在点D,使四面体ABCD有三个面是直角三角形;②不存在点D,使四面体ABCD是正三棱锥;③存在点D,使CD与AB垂直并相等;④存在无数个点D,使点O在四面体ABCD的外接球面上.则其中正确命题的序号是( )
,D为四面体OABC外一点.给出下列命题:①不存在点D,使四面体ABCD有三个面是直角三角形;②不存在点D,使四面体ABCD是正三棱锥;③存在点D,使CD与AB垂直并相等;④存在无数个点D,使点O在四面体ABCD的外接球面上.则其中正确命题的序号是( )
A.①② B.②③ C.①③ D.③④
 ,
, ,D为四面体OABC外一点.给出下列命题:①不存在点D,使四面体ABCD有三个面是直角三角形;②不存在点D,使四面体ABCD是正三棱锥;③存在点D,使CD与AB垂直并相等;④存在无数个点D,使点O在四面体ABCD的外接球面上.则其中正确命题的序号是( )
,D为四面体OABC外一点.给出下列命题:①不存在点D,使四面体ABCD有三个面是直角三角形;②不存在点D,使四面体ABCD是正三棱锥;③存在点D,使CD与AB垂直并相等;④存在无数个点D,使点O在四面体ABCD的外接球面上.则其中正确命题的序号是( )A.①② B.②③ C.①③ D.③④
D
试题分析:
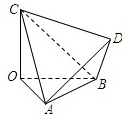
对于①,∵四面体OABC的三条棱OA,OB,OC两两垂直,OA=OB=2,OC=3,∴AC=BC=
 ,AB=2
,AB=2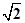 ,当四棱锥CABD与四面体OABC一样时,即取CD=3,AD=BD=2,四面体ABCD的三条棱DA、DB、DC两两垂直,此时点D,使四面体ABCD有三个面是直角三角形,故①不正确;对于②,由①知AC=BC=
,当四棱锥CABD与四面体OABC一样时,即取CD=3,AD=BD=2,四面体ABCD的三条棱DA、DB、DC两两垂直,此时点D,使四面体ABCD有三个面是直角三角形,故①不正确;对于②,由①知AC=BC= ,AB=2
,AB=2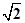 ,使AB=AD=BD,此时存在点D,CD=
,使AB=AD=BD,此时存在点D,CD= ,使四面体C-ABD是正三棱锥,故②不正确;对于③,取CD=AB,AD=BD,此时CD垂直面ABD,即存在点D,使CD与AB垂直并且相等,故③正确;对于④,先找到四面体OABC的内接球的球心P,使半径为r,只需PD=r即可,∴存在无数个点D,使点O在四面体ABCD的外接球面上,故④正确,故正确的命题有③④,故选D.
,使四面体C-ABD是正三棱锥,故②不正确;对于③,取CD=AB,AD=BD,此时CD垂直面ABD,即存在点D,使CD与AB垂直并且相等,故③正确;对于④,先找到四面体OABC的内接球的球心P,使半径为r,只需PD=r即可,∴存在无数个点D,使点O在四面体ABCD的外接球面上,故④正确,故正确的命题有③④,故选D.点评:本题考查棱锥的结构特征,同时考查了空间想象能力,转化与划归的思想,以及构造法的运用,属于中档题

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
 AB,ABED是边长为1的正方形,EB⊥底面ABC,若G,F分别是EC,BD的中点.
AB,ABED是边长为1的正方形,EB⊥底面ABC,若G,F分别是EC,BD的中点.
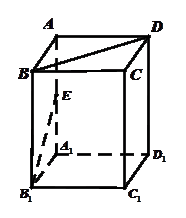
 的底面是边长为1的正方形,侧棱垂直底边ABCD四棱柱,
的底面是边长为1的正方形,侧棱垂直底边ABCD四棱柱, ,
,
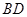 与B1E所成角的大小;
与B1E所成角的大小;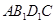 的体积.
的体积.  ,E,F分别为AB、CB中点,过直线EF作棱柱的截面,若截面与平面ABC所成的二面角的大小为60º,则截面的面积为( ).
,E,F分别为AB、CB中点,过直线EF作棱柱的截面,若截面与平面ABC所成的二面角的大小为60º,则截面的面积为( ).
 中,
中, ,
, ,点
,点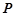 在
在 上,
上, 交
交 于
于 ,
, 交
交 于
于 .沿
.沿 将△
将△ 翻折成△
翻折成△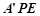 ,使平面
,使平面 平面
平面 将△
将△ 翻折成△
翻折成△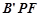 ,使平面
,使平面 平面
平面
 平面
平面 ,当
,当 为何值时,二面角
为何值时,二面角 的大小为
的大小为 ?
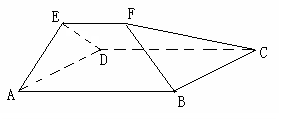
?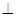 平面ABCD,EF∥AB, AB=2EF=2AD=4,
平面ABCD,EF∥AB, AB=2EF=2AD=4,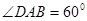 .
.
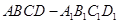 中,当底面四边形
中,当底面四边形 满足 时,有
满足 时,有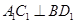 成立.(填上你认为正确的一个条件即可)
成立.(填上你认为正确的一个条件即可)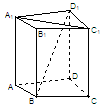
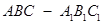 中,△
中,△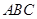 是边长为
是边长为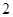 的等边三角形,
的等边三角形,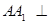 平面
平面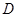 ,
,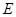 分别是
分别是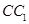 ,
,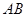 的中点.
的中点. 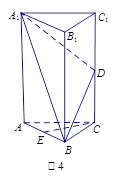
 ∥平面
∥平面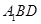 ;
;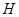 为
为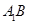 上的动点,当
上的动点,当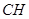 与平面
与平面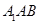 所成最大角的正切值为
所成最大角的正切值为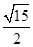 时,
时,