题目内容
3.已知函数f(x)=loga$\frac{x+1}{x-1}$(a>0,且a≠1)(1)判断f(x)的奇偶性并证明;
(2)若对于x∈[2,4],恒有f(x)>loga$\frac{m}{(x-1)•(7-x)}$成立,求m的取值范围.
分析 (1)根据函数奇偶性的定义进行判断.
(2)根据对数函数的单调性,将不等式恒成立进行转化,利用参数分离法进行求解即可.
解答 解:(1)因为$\frac{x+1}{x-1}$>解得x>1或x<-1,
所以函数f(x)的定义域为(-∞,-1)∪(1,+∞),
函数f(x)为奇函数,证明如下:
由(I)知函数f(x)的定义域关于原点对称,
又因为f(-x)=loga$\frac{-x+1}{-x-1}$=loga$\frac{x-1}{x+1}$=loga($\frac{x+1}{x-1}$)-1=-loga$\frac{x+1}{x-1}$=-f(x),
所以函数f(x)为奇函数…(4分)
(2)若对于x∈[2,4],f(x)>loga$\frac{m}{(x-1)•(7-x)}$恒成立
即loga$\frac{x+1}{x-1}$>loga$\frac{m}{(x-1)•(7-x)}$对x∈[2,4]恒成立
当a>1时,即$\frac{x+1}{x-1}$>$\frac{m}{(x-1)•(7-x)}$对x∈[2,4]成立.
则x+1>$\frac{m}{7-x}$,即(x+1)(7-x)>m成立,
设g(x)=(x+1)(7-x)=-(x-3)2+16,
因为x∈[2,4]
所以g(x)∈[15,16],
则0<m<15,
同理当0<a<1时,即$\frac{x+1}{x-1}$<$\frac{m}{(x-1)•(7-x)}$对x∈[2,4]成立.
则x+1<$\frac{m}{7-x}$,即(x+1)(7-x)<m成立,
设g(x)=(x+1)(7-x)=-(x-3)2+16,
因为x∈[2,4]
所以g(x)∈[15,16],
则m>16,
综上所述:a>1时,0<m<15,
0<a<1时,m>16 ….(12分)
点评 本题主要考查函数奇偶性的判断以及不等式恒成立问题问题,利用对数函数的单调性,利用参数分离法进行求解即可.

| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
| A. | $-\frac{{2\sqrt{5}}}{5}$ | B. | $-\frac{{\sqrt{5}}}{5}$ | C. | -2 | D. | -$\frac{1}{3}$ |
| A. | 对任意x∈R,都有x 2<ln2 | B. | 不存在x∈R,都有x 2<ln2 | ||
| C. | 存在x∈R,使得x 2≥ln2 | D. | 存在x∈R,使得x 2<ln2 |

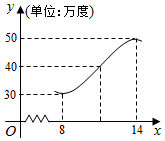 如图,某地夏天从8~14时用电量变化曲线近似满足函数y=Asin(ωx+φ)+b(ω>0,0<φ<π).
如图,某地夏天从8~14时用电量变化曲线近似满足函数y=Asin(ωx+φ)+b(ω>0,0<φ<π).