题目内容
19.已知动直线l0:ax+by+c-2=0(a>0,c>0)恒过点P(1,m)且Q(4,0)到动直线l0的最大距离为3,则$\frac{1}{2a}$+$\frac{2}{c}$的最小值为( )| A. | $\frac{9}{2}$ | B. | $\frac{9}{4}$ | C. | 1 | D. | 9 |
分析 由题意可得:可得a+bm+c-2=0.又Q(4,0)到动直线l0的最大距离为3,可得$\sqrt{(4-1)^{2}+{m}^{2}}$=3,解得m=0.a+c=2.再利用“乘1法”与基本不等式的性质即可得出.
解答 解:动直线l0:ax+by+c-2=0(a>0,c>0)恒过点P(1,m),∴a+bm+c-2=0.
又Q(4,0)到动直线l0的最大距离为3,
∴$\sqrt{(4-1)^{2}+{m}^{2}}$=3,解得m=0.
∴a+c=2.
则$\frac{1}{2a}$+$\frac{2}{c}$=$\frac{1}{2}$(a+c)$(\frac{1}{2a}+\frac{2}{c})$=$\frac{1}{2}(\frac{5}{2}+\frac{c}{2a}+\frac{2a}{c})$≥$\frac{1}{2}$$(\frac{5}{2}+2\sqrt{\frac{c}{2a}•\frac{2a}{c}})$=$\frac{9}{4}$,当且仅当c=2a=$\frac{4}{3}$时取等号.
故选:B.
点评 本题考查了直线方程、点到直线的距离公式、两点之间的距离公式、基本不等式的性质,考查了推理能力 与计算能力,属于中档题.

练习册系列答案
相关题目
14.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1、F2,过点F1且垂直于x轴的直线与该双曲线的左支交于A、B两点,AF2、BF2分别交y轴于P、Q两点,若△PQF2的周长为12,则ab取得最大值时双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\frac{3\sqrt{2}}{2}$ |
4.已知α,β为平面,a,b,c为直线,下列命题正确的是( )
| A. | a?α,若b∥a,则b∥α | B. | α⊥β,α∩β=c,b⊥c,则b⊥β | ||
| C. | a⊥b,b⊥c,则a∥c | D. | a∩b=A,a?α,b?α,a∥β,b∥β,则α∥β |
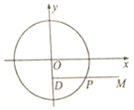 如图,已知DP⊥y轴,点D为垂足,点M在线段DP的延长线上,且满足|DP|=|PM|,当点P在圆x2+y2=3上运动时
如图,已知DP⊥y轴,点D为垂足,点M在线段DP的延长线上,且满足|DP|=|PM|,当点P在圆x2+y2=3上运动时