题目内容
抛物线y=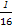
x2的焦点与双曲线
-
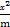=1的上焦点重合,则m= .
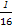x2的焦点与双曲线-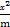=1的上焦点重合,则m= .13
因为抛物线y=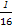x2的标准方程为x2=16y,焦点坐标为(0,4),又因为双曲线-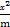=1的上焦点坐标为(0,
),依题意有4=,解得m=13.
【误区警示】本题易出现y=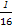x2的焦点为(0,
)的错误,原因是对抛物线的标准方程记忆不准确.
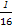x2的标准方程为x2=16y,焦点坐标为(0,4),又因为双曲线-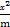=1的上焦点坐标为(0,),依题意有4=,解得m=13.【误区警示】本题易出现y=
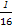x2的焦点为(0,)的错误,原因是对抛物线的标准方程记忆不准确.
练习册系列答案
相关题目
-
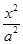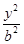=1(a>0,b>0)的离心率为2.若抛物线C2:x2=2py(p>0)的焦点到双曲线C1的渐近线的距离为2,则抛物线C2的方程为( )
y
y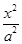
-
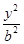=1(a>0,b>0)的两条渐近线均和圆C:x2+y2-6x+5=0相切,且双曲线的右焦点为圆C的圆心,则该双曲线的方程为( )
-
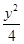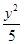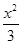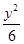=1
-
=1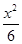
-
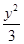=1
-
=1
的离心率
，则双曲线的渐近线方程为
-
=1(a>0,b>0)的左焦点且垂直于x轴的直线与双曲线相交于M,N两点,O为双曲线的中心,
·
=0,则双曲线的离心率为 .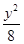
＝1 (x＞1) 
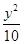＝1(x＞0)
的焦距是10，则实数
的值是（ ）
的焦距为
