题目内容
已知双曲线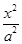 -
-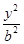 =1(a>0,b>0)的两条渐近线均和圆C:x2+y2-6x+5=0相切,且双曲线的右焦点为圆C的圆心,则该双曲线的方程为( )
=1(a>0,b>0)的两条渐近线均和圆C:x2+y2-6x+5=0相切,且双曲线的右焦点为圆C的圆心,则该双曲线的方程为( )
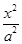 -
-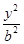 =1(a>0,b>0)的两条渐近线均和圆C:x2+y2-6x+5=0相切,且双曲线的右焦点为圆C的圆心,则该双曲线的方程为( )
=1(a>0,b>0)的两条渐近线均和圆C:x2+y2-6x+5=0相切,且双曲线的右焦点为圆C的圆心,则该双曲线的方程为( )A. - -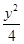 =1 =1 | B. - -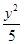 =1 =1 |
C.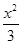 - -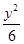 =1 =1 | D.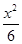 - -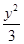 =1 =1 |
A
∵双曲线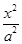 -
-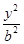 =1的渐近线方程为y=±
=1的渐近线方程为y=± x,
x,
圆C的标准方程为(x-3)2+y2=4,
∴圆心为C(3,0).
又渐近线方程与圆C相切,即直线bx-ay=0与圆C相切,
∴ =2,
=2,
∴5b2=4a2.①
又∵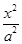 -
-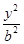 =1的右焦点F2(
=1的右焦点F2( ,0)为圆心C(3,0),
,0)为圆心C(3,0),
∴a2+b2=9.②
由①②得a2=5,b2=4.
∴双曲线的标准方程为 -
-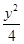 =1.故选A.
=1.故选A.
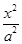 -
-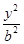 =1的渐近线方程为y=±
=1的渐近线方程为y=± x,
x,圆C的标准方程为(x-3)2+y2=4,
∴圆心为C(3,0).
又渐近线方程与圆C相切,即直线bx-ay=0与圆C相切,
∴
 =2,
=2,∴5b2=4a2.①
又∵
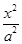 -
-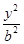 =1的右焦点F2(
=1的右焦点F2( ,0)为圆心C(3,0),
,0)为圆心C(3,0),∴a2+b2=9.②
由①②得a2=5,b2=4.
∴双曲线的标准方程为
 -
-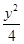 =1.故选A.
=1.故选A.
练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
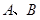 为两个定点,
为两个定点,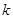 为非零常数,
为非零常数, ,则动点
,则动点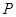 的轨迹为双曲线;②过定圆
的轨迹为双曲线;②过定圆 上一定点
上一定点 作圆的动点弦
作圆的动点弦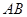 ,
, 为坐标原点,若
为坐标原点,若 则动点
则动点 是
是 的一内角,且
的一内角,且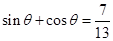 ,则
,则 表示焦点在
表示焦点在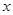 轴上的双曲线;④已知两定点
轴上的双曲线;④已知两定点 和一动点
和一动点 ,则点
,则点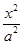 -
-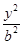 =1(a>0,b>0)的左焦点,B1B2是双曲线的虚轴,M是OB1的中点,过F、M的直线与双曲线C的一个交点为A,且
=1(a>0,b>0)的左焦点,B1B2是双曲线的虚轴,M是OB1的中点,过F、M的直线与双曲线C的一个交点为A,且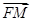 =2
=2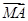 ,则双曲线C离心率是 .
,则双曲线C离心率是 .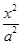 -
-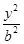 =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为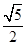 ,则C的渐近线方程为( )
,则C的渐近线方程为( ) x
x x
x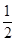 x
x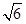
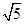
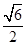
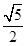
 -
- =1的左焦点,P,Q为C上的点.若PQ的长等于虚轴长的2倍,点A(5,0)在线段PQ上,则△PQF的周长为 .
=1的左焦点,P,Q为C上的点.若PQ的长等于虚轴长的2倍,点A(5,0)在线段PQ上,则△PQF的周长为 .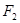 作垂直于实轴的弦
作垂直于实轴的弦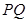 ,
, 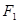 是另一焦点,若
是另一焦点,若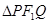 是钝角三角形,则双曲线的离心率
是钝角三角形,则双曲线的离心率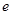 范围是( )
范围是( )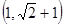


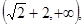
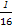 x2的焦点与双曲线
x2的焦点与双曲线 -
-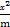 =1的上焦点重合,则m= .
=1的上焦点重合,则m= . 的焦点
的焦点 与双曲
与双曲 的右焦点重合,抛物线的准线与
的右焦点重合,抛物线的准线与 轴的交点为
轴的交点为 ,点
,点 在抛物线上且
在抛物线上且 ,则
,则


