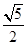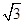题目内容
已知双曲线C1: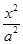 -
-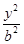 =1(a>0,b>0)的离心率为2.若抛物线C2:x2=2py(p>0)的焦点到双曲线C1的渐近线的距离为2,则抛物线C2的方程为( )
=1(a>0,b>0)的离心率为2.若抛物线C2:x2=2py(p>0)的焦点到双曲线C1的渐近线的距离为2,则抛物线C2的方程为( )
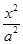 -
-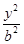 =1(a>0,b>0)的离心率为2.若抛物线C2:x2=2py(p>0)的焦点到双曲线C1的渐近线的距离为2,则抛物线C2的方程为( )
=1(a>0,b>0)的离心率为2.若抛物线C2:x2=2py(p>0)的焦点到双曲线C1的渐近线的距离为2,则抛物线C2的方程为( )A.x2= y y | B.x2= y y |
| C.x2=8y | D.x2=16y |
D
由e= =2得4=
=2得4= =1+
=1+ ,
,
∴ =3.
=3.
∴双曲线的渐近线方程为y=± x,抛物线x2=2py的焦点是(0,
x,抛物线x2=2py的焦点是(0, ),
),
它到直线y=± x的距离d=2=
x的距离d=2= =
= ,
,
∴p=8.
∴抛物线方程为x2=16y.
故选D.
 =2得4=
=2得4= =1+
=1+ ,
,∴
 =3.
=3.∴双曲线的渐近线方程为y=±
 x,抛物线x2=2py的焦点是(0,
x,抛物线x2=2py的焦点是(0, ),
),它到直线y=±
 x的距离d=2=
x的距离d=2= =
= ,
,∴p=8.
∴抛物线方程为x2=16y.
故选D.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
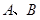 为两个定点,
为两个定点,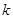 为非零常数,
为非零常数, ,则动点
,则动点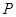 的轨迹为双曲线;②过定圆
的轨迹为双曲线;②过定圆 上一定点
上一定点 作圆的动点弦
作圆的动点弦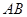 ,
, 为坐标原点,若
为坐标原点,若 则动点
则动点 是
是 的一内角,且
的一内角,且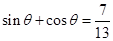 ,则
,则 表示焦点在
表示焦点在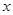 轴上的双曲线;④已知两定点
轴上的双曲线;④已知两定点 和一动点
和一动点 ,则点
,则点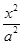 -
-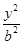 =1(a>0,b>0)的离心率为2,一个焦点与抛物线y2=16x的焦点相同,则双曲线的渐近线方程为( )
=1(a>0,b>0)的离心率为2,一个焦点与抛物线y2=16x的焦点相同,则双曲线的渐近线方程为( )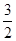 x
x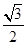 x
x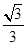 x
x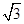 x
x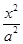 -
-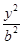 =1(a>0,b>0)的一个焦点,且双曲线的离心率为2,则该双曲线的方程为 .
=1(a>0,b>0)的一个焦点,且双曲线的离心率为2,则该双曲线的方程为 .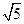 ,0),点P在双曲线上,且线段PF1的中点坐标为(0,2),则此双曲线的方程是( )
,0),点P在双曲线上,且线段PF1的中点坐标为(0,2),则此双曲线的方程是( )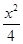 -y2=1
-y2=1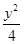 =1
=1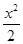 -
-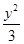 =1
=1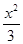 -
-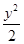 =1
=1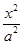 -
-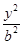 =1(a>0,b>0)的左焦点,B1B2是双曲线的虚轴,M是OB1的中点,过F、M的直线与双曲线C的一个交点为A,且
=1(a>0,b>0)的左焦点,B1B2是双曲线的虚轴,M是OB1的中点,过F、M的直线与双曲线C的一个交点为A,且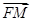 =2
=2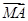 ,则双曲线C离心率是 .
,则双曲线C离心率是 .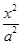 -
-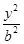 =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为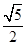 ,则C的渐近线方程为( )
,则C的渐近线方程为( ) x
x x
x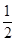 x
x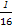 x2的焦点与双曲线
x2的焦点与双曲线 -
-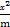 =1的上焦点重合,则m= .
=1的上焦点重合,则m= .
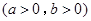 的渐近线方程是
的渐近线方程是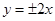 ,则其离心率为( )
,则其离心率为( )