题目内容
已知函数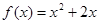 .
.
(Ⅰ)若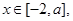 求
求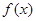 的值域;
的值域;
(Ⅱ)若存在实数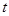 ,当
,当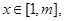
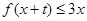 恒成立,求实数
恒成立,求实数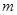 的取值范围.
的取值范围.
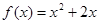 .
.(Ⅰ)若
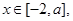 求
求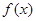 的值域;
的值域;(Ⅱ)若存在实数
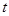 ,当
,当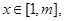
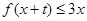 恒成立,求实数
恒成立,求实数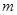 的取值范围.
的取值范围.(I)当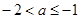 时,
时, 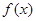 的值域为:
的值域为: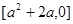 .当
.当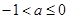 时,
时,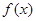 的值域为:
的值域为: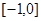 .当
.当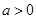 时,
时,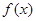 的值域为:
的值域为: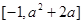 .(II)
.(II)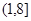 .
.
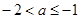 时,
时, 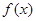 的值域为:
的值域为: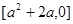 .当
.当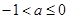 时,
时,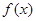 的值域为:
的值域为: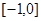 .当
.当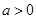 时,
时,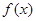 的值域为:
的值域为: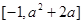 .(II)
.(II)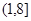 .
.试题分析:(I)由于
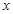 的范围含有参数
的范围含有参数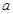 ,故结合抛物线的图象对
,故结合抛物线的图象对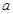 分情况进行讨论.
分情况进行讨论. (II)由
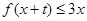 恒成立得:
恒成立得: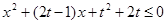 恒成立,
恒成立,令
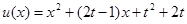 ,
,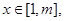 则只需
则只需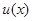 的最大值小于等于0.
的最大值小于等于0.由此得:
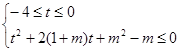 ,令
,令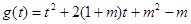
则原题可转化为:存在
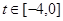 ,使得
,使得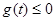 .这又需要
.这又需要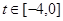 时
时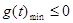 .接下来又对二次函数
.接下来又对二次函数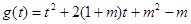 分情况讨论,从而求出实数
分情况讨论,从而求出实数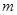 的取值范围.
的取值范围.试题解析:(I)由题意得:
当
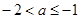 时,
时,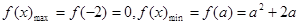 ,
,∴此时
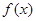 的值域为:
的值域为: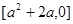 2分
2分当
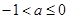 时,
时,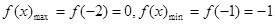 ,
,∴此时
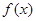 的值域为:
的值域为: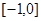 4分
4分当
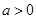 时,
时,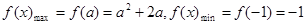 ,
,∴此时
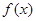 的值域为:
的值域为: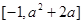 6分
6分(II)由
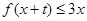 恒成立得:
恒成立得: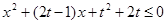 恒成立,
恒成立,令
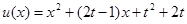 ,
,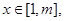 因为抛物线的开口向上,所以
因为抛物线的开口向上,所以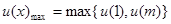 ,由
,由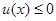 恒成立知:
恒成立知: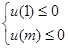 8分
8分化简得:
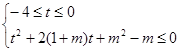 令
令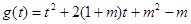
则原题可转化为:存在
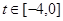 ,使得
,使得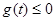 即:当
即:当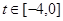 ,
,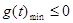 10分
10分∵
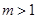 ,
,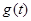 的对称轴:
的对称轴: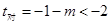
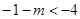 即:
即: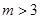 时,
时,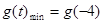
∴

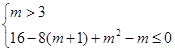 解得:
解得: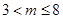
②当
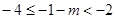 即:
即: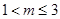 时,
时,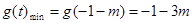
∴

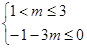 解得:
解得: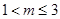
综上:
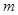 的取值范围为:
的取值范围为: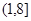 13分
13分法二:也可
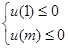 ,
,化简得:
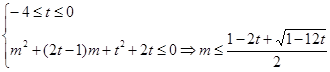 有解.
有解.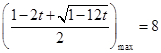 ,则
,则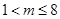 .
.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
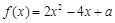 ,
,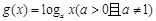 .
.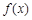 在
在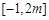 上不具有单调性,求实数
上不具有单调性,求实数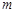 的取值范围;
的取值范围; 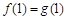 .
.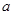 的值;
的值;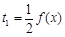 ,
,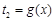 ,
,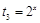 ,当
,当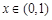 时,试比较
时,试比较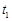 ,
,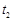 ,
,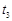 的大小.
的大小.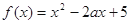 (
(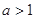 ).
).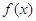 的定义域和值域均是
的定义域和值域均是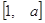 ,求实数
,求实数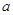 的值;
的值;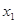 ,
,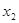
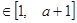 ,总有
,总有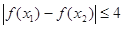 ,求实数
,求实数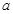 的取值范围.
的取值范围.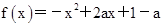 在
在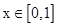 时有最大值2,求a的值.
时有最大值2,求a的值.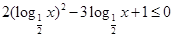 的解集为M,求当x∈M时函数
的解集为M,求当x∈M时函数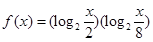 的最大、最小值.
的最大、最小值.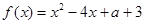 ,
,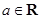 .
.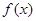 在
在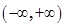 上至少有一个零点,求
上至少有一个零点,求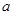 的取值范围;
的取值范围;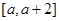 上的最大值为
上的最大值为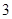 ,求
,求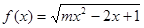 的定义域为R,则实数m的取值范围是( )
的定义域为R,则实数m的取值范围是( )



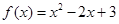 在区间
在区间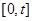 上有最大值3,最小值2,则
上有最大值3,最小值2,则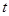 的取值范围是( )
的取值范围是( )


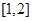
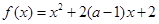 在区间
在区间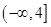 上是减函数,那么实数
上是减函数,那么实数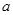 的取值范围是
的取值范围是