题目内容
已知函数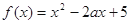 (
(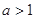 ).
).
(1)若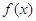 的定义域和值域均是
的定义域和值域均是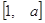 ,求实数
,求实数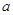 的值;
的值;
(2)若对任意的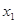 ,
,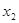
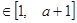 ,总有
,总有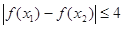 ,求实数
,求实数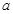 的取值范围.
的取值范围.
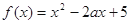 (
(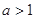 ).
).(1)若
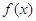 的定义域和值域均是
的定义域和值域均是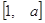 ,求实数
,求实数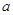 的值;
的值;(2)若对任意的
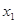 ,
,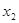
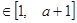 ,总有
,总有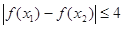 ,求实数
,求实数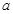 的取值范围.
的取值范围.(1) ;(2)
;(2)
 ;(2)
;(2)
试题分析:(1)求出二次函数的对称轴是关键.通过对称轴知道函数f(x)在
 上单调递减.在结合已知条件即可得两个等式.求出结论.
上单调递减.在结合已知条件即可得两个等式.求出结论.(2)条件
 表示的含义是函数f(x)在
表示的含义是函数f(x)在 上的最大值与最小值的差小于或等于4.因为函数f(x)的对称轴为
上的最大值与最小值的差小于或等于4.因为函数f(x)的对称轴为 .所以要将
.所以要将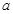 的值分两类
的值分两类 .再根据单调性即可求得
.再根据单调性即可求得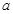 的范围.本题的函数的背景是二次函数所以抓住对称轴展开研究函数的最值单调性.同时分类的思想是解题的关键.
的范围.本题的函数的背景是二次函数所以抓住对称轴展开研究函数的最值单调性.同时分类的思想是解题的关键.试题解析:(1)因为
 .所以f(x)在
.所以f(x)在 是减函数,又定义域和值域为
是减函数,又定义域和值域为 所以
所以 .即
.即 .解得
.解得 .
.(2)若
 .又
.又 ,且
,且 .所以
.所以 .
. .因为对任意的
.因为对任意的 .总有
.总有 .所以
.所以 .即
.即 .解得
.解得 .又
.又 .所以
.所以 .若
.若 .
. .
. .
. 显然成立.综上
显然成立.综上 .
.
练习册系列答案
相关题目
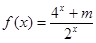 是奇函数.
是奇函数.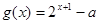 .若函数
.若函数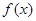 与
与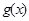 的图象至少有一个公共点.求实数a的取值范围.
的图象至少有一个公共点.求实数a的取值范围. 对一切
对一切 恒成立,试确定实数
恒成立,试确定实数 的取值范围.
的取值范围. 的图像顶点为
的图像顶点为 ,且图像在
,且图像在 轴截得的线段长为6.
轴截得的线段长为6. ;
; 在区间
在区间 上单调,求
上单调,求 的范围.
的范围.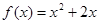 .
.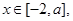 求
求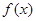 的值域;
的值域;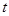 ,当
,当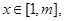
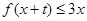 恒成立,求实数
恒成立,求实数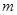 的取值范围.
的取值范围. x2-x+
x2-x+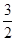 是[1,b]上的“四维光军”函数,求常数b的值;
是[1,b]上的“四维光军”函数,求常数b的值; 是区间[a,b]上的“四维光军”函数?若存在,求出a,b的值,否则,请说明理由.
是区间[a,b]上的“四维光军”函数?若存在,求出a,b的值,否则,请说明理由.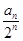 ,求Tn.
,求Tn. 是方程
是方程 的两根,且
的两根,且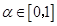 ,
, ,
, ,求
,求 的最大值与最小值之和为( ).
的最大值与最小值之和为( ).
 在区间[0,2]上有两个零点,则实数
在区间[0,2]上有两个零点,则实数 的取值范围是________ .
的取值范围是________ .