题目内容
抛物线y=
x2的焦点坐标为（ ）
| 1 |
| a |
A、(0，-
| ||
B、(0，
| ||
C、(
| ||
D、(
|
考点：抛物线的标准方程
专题：圆锥曲线的定义、性质与方程
分析：利用抛物线的简单性质求解．
解答：
解：∵抛物线y=
x2的标准方程为x2=ay，
∴抛物线y=
x2的焦点坐标为（0，
）．
故选：B．
| 1 |
| a |
∴抛物线y=
| 1 |
| a |
| a |
| 4 |
故选：B．
点评：本题考查抛物线的焦点坐标的求法，是基础题，解题时要认真审题．
练习册系列答案
相关题目
已知a、b为正实数，直线y=x-a与曲线y=ln（x+b）相切，则
的取值范围是（ ）
| a2 |
| 2+b |
A、（0，
| ||
| B、（0，1） | ||
| C、（0，+∞） | ||
| D、[1，+∞） |
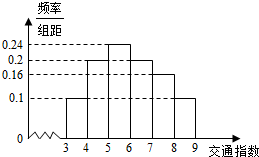交通指数是交通拥堵指数的简称，是综合反映道路网畅通或拥堵的概念．记交通指数为T，其范围为[0，10]，分别有5个级别：T∈[0，2）畅通；T∈[2，4）基本畅通；T∈[4，6）轻度拥堵；T∈[6，8）中度拥堵；T∈[8，10]严重拥堵．早高峰时段（T≥3），从贵阳市交通指挥中心随机选取了二环以内50个交通路段，依据交通指数数据绘制的直方图如图所示：