题目内容
已知椭圆| x2 | 4 |
(1)当直线AM的斜率为1时,求点M的坐标;
(2)当直线AM的斜率变化时,直线MN是否过x轴上的一定点,若过定点,请给出证明,并求出该定点,若不过定点,请说明理由.
分析:(1)根据直线AM的斜率为1时,得出直线AM:y=x+2,代入椭圆方程并化简得:5x2+16x+12=0,解得点M的坐标即可;(2)对于是否过x轴上的一定点问题,可先假设存在,设直线AM的斜率为k,则AM:y=k(x+2),将直线的方程代入椭圆的方程,消去y得到关于x的一元二次方程,再结合根系数的关系即可求得P点的坐标,从而解决问题.
解答:解:(1)直线AM的斜率为1时,直线AM:y=x+2,(1分)
代入椭圆方程并化简得:5x2+16x+12=0,(2分)
解之得x1=-2,x2=-
,∴M(-
,
).(4分)
(2)设直线AM的斜率为k,则AM:y=k(x+2),
则
化简得:(1+4k2)x2+16k2x+16k2-4=0.(6分)
∵此方程有一根为-2,∴xM=
,(7分)
同理可得xN=
.(8分)
由(1)知若存在定点,则此点必为P(-
,0).(9分)
∵kMP=
=
=
,(11分)
同理可计算得kPN=
.(13分)
∴直线MN过x轴上的一定点P(-
,0).(16分)
代入椭圆方程并化简得:5x2+16x+12=0,(2分)
解之得x1=-2,x2=-
| 6 |
| 5 |
| 6 |
| 5 |
| 4 |
| 5 |
(2)设直线AM的斜率为k,则AM:y=k(x+2),
则
|
∵此方程有一根为-2,∴xM=
| 2-8k2 |
| 1+4k2 |
同理可得xN=
| 2k2-8 |
| k2+4 |
由(1)知若存在定点,则此点必为P(-
| 6 |
| 5 |
∵kMP=
| yM | ||
xM+
|
k(
| ||||
|
| 5k |
| 4-4k2 |
同理可计算得kPN=
| 5k |
| 4-4k2 |
∴直线MN过x轴上的一定点P(-
| 6 |
| 5 |
点评:本题考查直接法求轨迹方程、直线与抛物线的位置关系、直线过定点问题.考查推理能力和运算能力.

练习册系列答案
相关题目
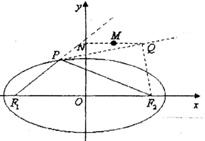 如图,已知椭圆
如图,已知椭圆