题目内容
15.设i是虚数单位,则复数$\frac{(1+i)^{2}}{1-i}$=( )| A. | 1+i | B. | 1-i | C. | -1-i | D. | -1+i |
分析 直接利用复数的除法与乘方运算法则化简求解即可.
解答 解:复数$\frac{(1+i)^{2}}{1-i}$=$\frac{2i(1+i)}{(1-i)(1+i)}$=i(1+i)=-1+i.
故选:D.
点评 本题考查复数的代数形式的混合运算,基本知识的考查.

练习册系列答案
相关题目
6.若实数a,b在区间[0,$\sqrt{2}$]上取值,则函数f(x)=$\frac{2}{3}$ax3+bx2+ax在R上有两个相异极值点的概率是( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | $\frac{\sqrt{2}}{8}$ | D. | $\frac{1}{2}$ |
3.用数学归纳法证明不等式$\frac{n+2}{2}$<1+$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+…+$\frac{1}{{2}^{n}}$<n+1(n>1,n∈N*)的过程中,当n=2时,中间式子为( )
| A. | 1 | B. | 1+$\frac{1}{2}$ | C. | 1+$\frac{1}{2}$+$\frac{1}{3}$ | D. | 1+$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$ |
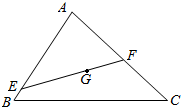 如图,G是△ABC的重心,过G的直线与边AB,AC分别相交于点E,F,若AE=mAB,AF=nAC(mn≠0),求$\frac{1}{m}$+$\frac{1}{n}$的值.
如图,G是△ABC的重心,过G的直线与边AB,AC分别相交于点E,F,若AE=mAB,AF=nAC(mn≠0),求$\frac{1}{m}$+$\frac{1}{n}$的值.