题目内容
已知集合M={x|x≠1,x∈R}∪{y|y≠2,y∈R},集合P={x|x<1或1<x<2或x>2},则M与P之间的关系是( )
| A、M?P | B、P?M |
| C、P=M | D、M∩P=∅ |
考点:集合的包含关系判断及应用
专题:集合
分析:本题的重点是明确集合M={x|x≠1,x∈R}∪{y|y≠2,y∈R}和集合P={x|x<1或1<x<2或x>2},的意义,以及考查两个集合之间的包含关系.
解答:
解:∵集合P={x|x<1或1<x<2或x>2}
∴P={x|x≠1且x≠2,x∈R}
∵M={x|x≠1,x∈R}∪{y|y≠2,y∈R},
∴M=R
∴P?M
故选B
∴P={x|x≠1且x≠2,x∈R}
∵M={x|x≠1,x∈R}∪{y|y≠2,y∈R},
∴M=R
∴P?M
故选B
点评:本题考查集合之间的关系,是一道高考常见的题目.

练习册系列答案
相关题目
下列函数中,在区间(0,2)上是增函数的是( )
| A、y=x2-4x+5 | ||
B、y=
| ||
| C、y=2-x | ||
D、y=log
|
已知P(4,-1),F为抛物线y2=8x的焦点,M为此抛物线上的点,则|MP|+|MF|的最小值为( )
| A、4 | B、5 | C、6 | D、7 |
已知点(-3,1)和(0,-2)在直线x-y-a=0的一侧,则a的取值范围是( )
| A、(-2,4) |
| B、(-4,2) |
| C、(-∞,-2)∪(2,+∞) |
| D、(-∞,-4)∪(2,+∞) |
已知圆(x-2)2+(y-1)2=1上点P(x,y),t=
,则t的取值范围是( )
| ||
| x |
| A、(0,1] | ||||||||
B、[-
| ||||||||
C、(-∞,
| ||||||||
| D、[-1,1] |
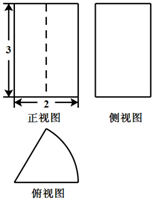 某由圆柱切割获得的几何体的三视图如图所示,其中俯视图是中心角为60°的扇形,则该几何体的体积为( )
某由圆柱切割获得的几何体的三视图如图所示,其中俯视图是中心角为60°的扇形,则该几何体的体积为( )A、
| ||
B、
| ||
| C、π | ||
| D、2π |
下列曲线的离心率是
的是( )
| ||
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|