题目内容

17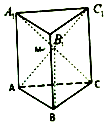．在三棱柱ABC-A1B1C1中，各侧面均为正方形，侧面AA1C1C的对角线相交于点M，则BM与平面ABC所成角的大小是（　　）
A．30°B．45°C．60°D．90°

分析 先确定BM与平面ABC所成角，再在直角三角形中求解即可．

解答 解：取AC的中点O，连接OM，则BO⊥平面AA1C1C，所以∠MBO为BM与平面ABC所成角．
设正方形的边长为2a，则OM=a，BO=$\sqrt{3}$a，∴tan∠MBO=$\frac{\sqrt{3}}{3}$
∴∠MBO=30°
故选A．

点评 本题考查线面角，考查学生的计算能力，正确作出线面角是关键．

练习册系列答案
相关题目
7．在公比为2的等比数列{an}中，a1a3=6a2，则a4等于（　　）
A．4B．8C．12D．24
8．复数z满足（z+2i）i=3-i，则|z|=$\sqrt{26}$．
5．已知a=${（\frac{1}{e}）}^{x}$，b=x2，c=lnx，其中e为自然对数的底数，则当x=e时，a，b，c的大小关系为（　　）
A．a＜b＜cB．a＜c＜bC．c＜b＜aD．c＜a＜b
12．已知定义域为[0，e]的函数f（x）同时满足：
①对于任意的x∈[0，e]，总有f（x）≥0；
②f（e）=e；
③若x1≥0，x2≥0，x1+x2≤e，则恒有f（x1+x2）≥f（x1）+f（x2）．
（1）求f（0）的值；
（2）证明：不等式f（x）≤e对任意x∈[0，e]恒成立；
（3）若对于任意x∈[0，e]，总有4f2（x）-4（2e-a）f（x）+4e2-4ea+1≥0，求实数a的取值范围．
2．大冶至武汉的城际列车C5502在黄石市辖区内设有2个停靠站，在鄂州市辖区内设有4个停靠站，为了了解该线路运营状况，交通管理部门计划从这6个车站中任选2站调研．
（1）求两个辖区各选1站的概率；
（2）求鄂州市辖区内至少选中1个车站的概率．
9．在等比数列{an}中，若a3，a7是方程x2-4x+3=0的两根，则a5=（　　）
A．±$\sqrt{3}$B．-$\sqrt{3}$C．$\sqrt{3}$D．±3
6．大西洋鲑鱼每年都要逆流而上，游回产地产卵，研究鲑鱼的科学家发现鲑鱼的游速可以表示为函数v=$\frac{1}{2}$log3$\frac{O}{100}$，单位是m/s，其中O表示鱼的耗氧量的单位数．
（1）当一条鱼的耗氧量是900个单位时，它的游速是多少？
（2）若鱼的游速范围是[0，$\frac{3}{2}$]，求鱼耗氧量的单位数的取值范围．
19．如图，在正三棱柱ABC-A1B1C1中，AB=4，AA1=6，E，F分别为BB1，AC的中点．
（1）求证：平面A1EC⊥平面ACC1A1；
（2）求几何体AA1EBC的体积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网