题目内容
12.已知定义域为[0,e]的函数f(x)同时满足:①对于任意的x∈[0,e],总有f(x)≥0;
②f(e)=e;
③若x1≥0,x2≥0,x1+x2≤e,则恒有f(x1+x2)≥f(x1)+f(x2).
(1)求f(0)的值;
(2)证明:不等式f(x)≤e对任意x∈[0,e]恒成立;
(3)若对于任意x∈[0,e],总有4f2(x)-4(2e-a)f(x)+4e2-4ea+1≥0,求实数a的取值范围.
分析 (1)令x1=0,x2=0代入即可得到答案,
(2)用定义确定函数f(x)在[0,e]上是单调递增的,求出函数的最值即可,
(3)先根据函数f(x)的单调性确定函数f(x)的取值范围,再分离参数的方法将a表示出来用基本不等式求出a的范围.
解答 解:(1)令x1=0,x2=0,得f(0)≤0,
又对于任意的x∈[0,e],总有f(x)≥0,
∴f(0)=0,
(2)证明:设0≤x1≤x2≤e,则x2-x1∈(0,e]
∴f(x2)-f(x1)=f((x2-x1)+x1)-f(x1)≥f(x2-x1)+f(x1)-f(x1)=f(x2-x1)≥0,
∴f(x2)≥f(x1),
∴f(x)在[0,e]上是单调递增的,
∴f(x)≤f(e)=e,
(3)∵f(x)在[0,e]上是增函数,
∴f(x)∈[0,e],
∵4f2(x)-4(2e-a)f(x)+4e2-4ea+1≥0,
∴4f2(x)-8ef(x)+4e2+1≥4a[e-f(x)],
当f(x)≠e时,
a≤$\frac{4{f}^{2}(x)-8ef(x)+4{e}^{2}+1}{4[e-f(x)]}$,
令y=$\frac{4{f}^{2}(x)-8ef(x)+4{e}^{2}+1}{4[e-f(x)]}$=$\frac{4[e-f(x)]^{2}+1}{4[e-f(x)]}$=e-f(x)+$\frac{1}{4[e-f(x)]}$≥e,当且f(x)=e-$\frac{1}{2}$时取等号,
∴a≤e,
当f(x)=e时,4f2(x)-4(2e-a)f(x)+4e2-4ea+1=4e2-4(2e-a)e+4e2-4ea+1=1≥0恒成立,
综上所述a≤e.
点评 本题考查了抽象函数的问题,以及函数的单调性和函数的最值,以及参数的取值范围,考查了学生的运算能力和转化能力,属于中档题.

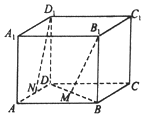 如图所示,在正方体ABCD-A1B1C1D1中,己知棱长为a,M,N分别是BD和AD的中点,则B1M与D1N所成角的余弦值为( )
如图所示,在正方体ABCD-A1B1C1D1中,己知棱长为a,M,N分别是BD和AD的中点,则B1M与D1N所成角的余弦值为( )| A. | -$\frac{\sqrt{15}}{15}$ | B. | $\frac{\sqrt{30}}{10}$ | C. | -$\frac{\sqrt{30}}{10}$ | D. | $\frac{\sqrt{15}}{15}$ |
| A. | $\frac{{\sqrt{3}}}{8}$ | B. | $\frac{{\sqrt{15}}}{8}$ | C. | $\frac{{2\sqrt{39}}}{13}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
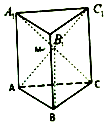 在三棱柱ABC-A1B1C1中,各侧面均为正方形,侧面AA1C1C的对角线相交于点M,则BM与平面ABC所成角的大小是( )
在三棱柱ABC-A1B1C1中,各侧面均为正方形,侧面AA1C1C的对角线相交于点M,则BM与平面ABC所成角的大小是( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
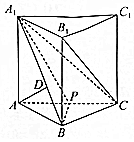 如图,直三棱柱ABC-A1B1C1中,AD⊥平面A1BC,其垂足D落在直线A1B上,P为AC的中点.
如图,直三棱柱ABC-A1B1C1中,AD⊥平面A1BC,其垂足D落在直线A1B上,P为AC的中点.