题目内容
10．在△ABC中，A=60°，AB=2，且△ABC的面积为2$\sqrt{3}$，则BC边的长为（ ）| A． | $\sqrt{7}$ | B． | 2$\sqrt{3}$ | C． | 3$\sqrt{7}$ | D． | 7 |
分析 利用三角形的面积求出AC，然后利用余弦定理求解即可．
解答 解：在△ABC中，A=60°，AB=2，且△ABC的面积为2$\sqrt{3}$，
可得$\frac{1}{2}AB•ACsinA=\frac{1}{2}×2×AC×\frac{\sqrt{3}}{2}$=2$\sqrt{3}$，
解得AC=4．
由余弦定理可得：BC=$\sqrt{{AB}^{2}+{AC}^{2}-2AB•ACcos60°}$=$\sqrt{4+16-2×4×2×\frac{1}{2}}$=$\sqrt{12}$=2$\sqrt{3}$．
故选：B．
点评 本题考查余弦定理以及三角形的面积的求法，考查计算能力．
练习册系列答案
相关题目
1．已知函数y=Asin（ωx+φ）（x∈R）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的图象如图所示，则（ ）
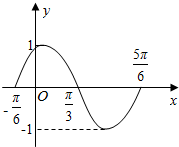
| A． | y=sin（x-$\frac{π}{6}$） | B． | y=sin（2x+$\frac{π}{3}$） | C． | y=-sin（2x+$\frac{π}{6}$） | D． | y=sin（2x+$\frac{π}{6}$） |