题目内容
4.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0.b>0)的右焦点为F2,M是双曲线C在第一象限上一点,N与M关于原点对称,MF2交双曲线C于另一点P,NF2⊥PF2,|NF2|=|PF2|,则双曲线C的渐近线为( )| A. | y=±2x | B. | y=±4x | C. | y=±$\frac{\sqrt{6}}{2}$x | D. | y=±$\frac{\sqrt{10}}{2}$x |
分析 设|NF2|=t,可得|PF2|=t,连接MF1,NF1,可得|MF1|=t,由双曲线的定义可得,|MF1|-|MF2|=2a,即有|MF2|=t-2a,再由勾股定理,可得t,再由|PF1|=t+2a,在直角三角形MPF1中,运用勾股定理,可得t,解方程可得a,b的关系,即可得到所求渐近线方程.
解答 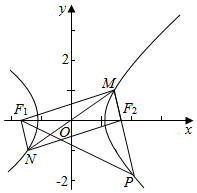 解:设|NF2|=t,可得|PF2|=t,
解:设|NF2|=t,可得|PF2|=t,
连接MF1,NF1,可得|MF1|=t,
由双曲线的定义可得,|MF1|-|MF2|=2a,
即有|MF2|=t-2a,
由NF2⊥PF2,可得t2+(t-2a)2=4c2=4a2+4b2,
解得t=a+$\sqrt{{a}^{2}+2{b}^{2}}$,
连接PF1,可得|PF1|-|PF2|=2a,
即有|PF1|=t+2a,在直角三角形MPF1中,可得
(t+2a)2=t2+(2t-2a)2,
解得t=3a,
由a+$\sqrt{{a}^{2}+2{b}^{2}}$=3a,化为2b2=3a2,
即为b=$\frac{\sqrt{6}}{2}$a,
可得渐近线方程为y=±$\frac{b}{a}$x,
即为y=±$\frac{\sqrt{6}}{2}$x.
故选:C.
点评 本题考查双曲线的渐近线方程的求法,注意运用双曲线的定义和勾股定理,考查化简整理的运算能力,属于中档题.

练习册系列答案
相关题目
15.曲线(x+2y+a)(x2-y2)=0为平面上交于一点的三条直线的充要条件是( )
| A. | a=0 | B. | a=1 | C. | a=-1 | D. | a∈R |
12.设集合A={a,a2,-2},B={2,4},A∩B={4},则a=( )
| A. | 2 | B. | -2 | C. | 4 | D. | $\sqrt{2}$ |
19.过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点F1作圆x2+y2=a2的切线,并延长交双曲线右支于点P,过右焦点F2作圆的切线交F1P于M,且M为F1P的中点,则双曲线的离心率e∈( )
| A. | (1,$\sqrt{2}$) | B. | ($\sqrt{2}$,$\sqrt{3}$) | C. | ($\sqrt{3},2$) | D. | (2,$\sqrt{5}$) |
9.设等差数列{an}的前n项和为Sn,且满足S2016>0,S2017<0,对任意正整数n,都有|an|≥|ak|,则k的值为( )
| A. | 1006 | B. | 1007 | C. | 1008 | D. | 1009 |
16.设函数f(x)=-|x|,g(x)=lg(ax2-4x+1),若对任意x1∈R,都存在x2∈R,使f(x1)=g(x2),则实数a的取值范围为( )
| A. | (-∞,4] | B. | (0,4] | C. | (-4,0] | D. | [4,+∞) |
13.若平面向量$\overrightarrow{a}$在$\overrightarrow{b}$方向上的投影为2,且$\overrightarrow{b}$=(-1,3),则$\overrightarrow{a}$$•\overrightarrow{b}$=( )
| A. | $\sqrt{10}$ | B. | 10 | C. | 2$\sqrt{10}$ | D. | 20 |