题目内容
已知函数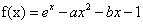 ,其中
,其中 ,
, …为自然对数的底数.(1)设
…为自然对数的底数.(1)设 是函数
是函数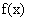 的导函数,求函数
的导函数,求函数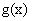 在区间
在区间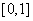 上的最小值;
上的最小值;
(2)若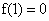 ,函数
,函数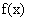 在区间
在区间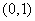 内有零点,证明:
内有零点,证明: .
.
[解析] (1)由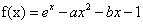 ,得
,得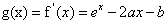 ,所以
,所以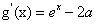

当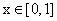 ]时,
]时,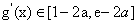 .
.
当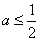 时,
时, ,所以
,所以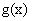 在
在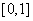 上单调递增,因此
上单调递增,因此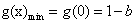 ;
;
当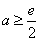 时,
时, ,所以
,所以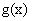 在
在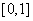 上单调递减,因此
上单调递减,因此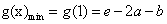 ;
;
当 时,令
时,令 ,得
,得 ,
,
所以函数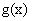 在区间
在区间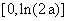 上单调递减,在区间
上单调递减,在区间 上单调递增,
上单调递增,
于是,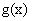 在
在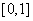 上的最小值是
上的最小值是 .
.
综上所述,当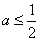 时,
时,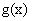 在
在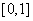 上的最小值是
上的最小值是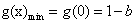 ;
;
当 时,
时,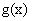 在
在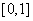 上的最小值是
上的最小值是 ;
;
当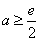 时,
时,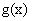 在
在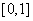 上的最小值是
上的最小值是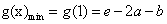 .
.
(2)证明:设 为
为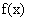
 在区间
在区间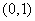 内的一个零点,则由
内的一个零点,则由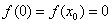 可知,
可知,
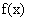 在区间
在区间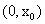 上不可能单调递增,也不可能单调递减.
上不可能单调递增,也不可能单调递减.
则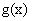 不可能恒为正,也不可能恒为负.故
不可能恒为正,也不可能恒为负.故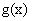 在区间
在区间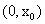 )内存在零点x1.
)内存在零点x1.
同理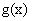 在区间
在区间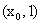 内存在零点x2.故
内存在零点x2.故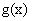 在区间
在区间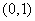 )内至少有两个零点.
)内至少有两个零点.
由(1)知,当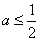 时,
时,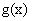 在
在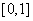 上单调递增,故
上单调递增,故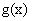 在
在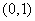 内至多有一个零点;
内至多有一个零点;
当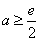 时,
时,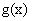 在
在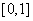 上单调递减,故
上单调递减,故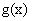 在
在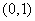 内至多有一个零点,不合题意.
内至多有一个零点,不合题意.
所以 .
.
此时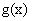 在区间
在区间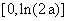 上单调递减,在区间
上单调递减,在区间 上单调递增.
上单调递增.
因此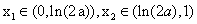 ,必有
,必有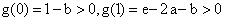
由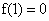 ,有
,有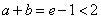 ,
,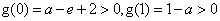
解得 所以,函数
所以,函数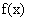 在区间(0,1)内有零点时,
在区间(0,1)内有零点时, .
.

练习册系列答案
相关题目
 的各项均为正数,且
的各项均为正数,且 ,则
,则 .
.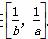 .若0<a<b≤2,求a、b的值.
.若0<a<b≤2,求a、b的值. ,若对任意
,若对任意 都有
都有 ,则
,则 的取值范围是 .
的取值范围是 . 在R上单调递增,则
在R上单调递增,则 的最小值为 .
的最小值为 . 的终边所在直线经过点
的终边所在直线经过点 ,则
,则 ______.
______. 上递减,且在该区间上有最小值1,则ω的值是______.
上递减,且在该区间上有最小值1,则ω的值是______. =________.
=________.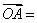 a + b,
a + b, a + 2b,
a + 2b, a + 3b (其中a 、b是两个任意非零向量) ,试求m、n之间的关系.
a + 3b (其中a 、b是两个任意非零向量) ,试求m、n之间的关系.