题目内容
已知f(x)是定义在R上的奇函数,当x≥0时f(x)=2x-x2.
(1)求函数f(x)的表达式并画出其大致图象;
(2)若当x∈[a,b]时,f(x)∈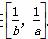 .若0<a<b≤2,求a、b的值.
.若0<a<b≤2,求a、b的值.
解析:
(1)当x<0时,f(x)=-f(-x)=-(-2x-x2)=x2+2x,
∴f(x)= ,
,
f(x)的大致图象如右:
(2)①0<a<b<1时,f(x)为增函数, ,
,
即2ab-a2b=2ab-ab2=1,得a=b,与a<b矛盾.
②1≤a<b≤2时,f(x)为减函数,
 ③0<a≤1<b<2时,由图象知f(1)=
③0<a≤1<b<2时,由图象知f(1)= =1,
=1,
得a=1,由 a<b,知1<b<2,此时与②一样.
a<b,知1<b<2,此时与②一样.
综上:a=1,b= .
.

练习册系列答案
相关题目
 与圆
与圆 心为
心为 的圆
的圆 相交于
相交于 两点,且
两点,且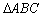 为等边三角形,则实数
为等边三角形,则实数 ________.
________.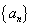 和
和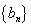 满足
满足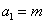 ,
, 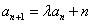 ,
,  .
.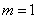 时,求证: 对于任意的实数
时,求证: 对于任意的实数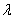 ,
,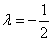 时,试判断
时,试判断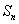 为数列
为数列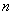 项和,在(Ⅱ)的条件下,是否存在实数
项和,在(Ⅱ)的条件下,是否存在实数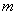 ,使得对任意的正整数
,使得对任意的正整数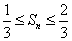 ?若存在,请求出
?若存在,请求出 (n∈Z)的图象关于y轴对称,且在(0,+∞)上是减函数,则n的值为________.
(n∈Z)的图象关于y轴对称,且在(0,+∞)上是减函数,则n的值为________. 的取值范围是________.
的取值范围是________. 在
在 上是增函数,若
上是增函数,若 ,则不等式
,则不等式 解集是 .
解集是 .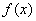 在R上满足
在R上满足 ,则
,则 在点
在点 处的切线是_______.
处的切线是_______.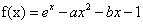 ,其中
,其中 ,
,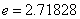 …为自然对数的底数.(1)设
…为自然对数的底数.(1)设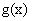 是函数
是函数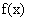 的导函数,求函数
的导函数,求函数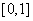 上的最小值;
上的最小值;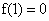 ,函数
,函数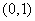 内有零点,证明:
内有零点,证明: .
.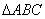 中,
中, 边上的中线
边上的中线 长为3,且
长为3,且 ,
, .
. 的值;
的值; 边的长.
边的长. 