题目内容
【题目】已知点![]() 在函数
在函数![]() 的图象上,数列
的图象上,数列![]() 的前
的前![]() 项和为
项和为![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() 是
是![]() 与
与![]() 的等差中项.
的等差中项.
(![]() )求数列
)求数列![]() 的通项公式.
的通项公式.
(![]() )设
)设![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() .求数列
.求数列![]() 的前
的前![]() 项和
项和![]() .
.
(![]() )在(
)在(![]() )的条件下,设
)的条件下,设![]() 是定义在正整数集上的函数,对于任意的正整数
是定义在正整数集上的函数,对于任意的正整数![]() ,
,![]() ,恒有
,恒有![]() 成立,且
成立,且![]() (
(![]() 为常数,
为常数,![]() ),试判断数列
),试判断数列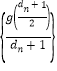 是否为等差数列,并说明理由.
是否为等差数列,并说明理由.
【答案】(1) ![]() ;(2)
;(2) ![]() ;(3)见解析.
;(3)见解析.
【解析】分析:(1)本题考查求数列的通项公式,用数列的前n项和求是列的通项公式,注意对于第一项的验证,又根据等比中项解决问题,这一道题目比较困难,第一问考查的内容较多.
(2)构造新数列,构造数列时按照一般的方式来整理,整理后发现结果比较简单,利用等比数列的前n项和公式求数列的和.
(3)本题证明数列是一个等差数列,应用等差数列的定义来证明,只要数列的连续两项之差是一个常数,问题得证,证明是一个常数的过程是一个数列和函数综合的过程,用到所给的函数的性质.
详解:
(![]() )依题意得
)依题意得![]() ,故
,故![]() .
.
又![]() ,即
,即![]() ,
,
所以,当![]() 时,
时,![]() .
.
又![]() 也适合上式,
也适合上式,
故![]() .
.
(![]() )因为
)因为![]() ,
,
![]() ,因此
,因此![]() .
.
由于![]() ,所以
,所以![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列.
的等比数列.
所以![]() ,所以
,所以![]() .
.
所以![]() .
.
(![]() )方法一:
)方法一:
![]() ,
,
则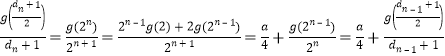 .
.
所以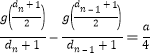 .
.
因为已知![]() 为常数,则数列
为常数,则数列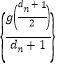 是等差数列.
是等差数列.
方法二:
因为![]() 成立,且
成立,且![]() ,
,
所以![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
所以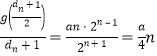 .
.
所以数列 是等差数列.
是等差数列.

练习册系列答案
相关题目