题目内容
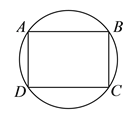
【题目】矩形![]() 中,
中, ![]() ,
, ![]() 边所在直线的方程为
边所在直线的方程为![]() ,点
,点![]() 在
在![]() 边所在直线上.
边所在直线上.
(![]() )求
)求![]() 边所在直线的方程.
边所在直线的方程.
(![]() )求矩形
)求矩形![]() 外接圆的方程.
外接圆的方程.
(![]() )若过点
)若过点![]() 作题(
作题(![]() )中的圆的切线,求切线的方程.
)中的圆的切线,求切线的方程.
【答案】(![]() )
)![]() (
(![]() )
)![]() (
(![]() )
)![]() 或
或![]()
【解析】试题分析:
(1)根据直线![]() 的斜率及
的斜率及![]() 可得直线
可得直线![]() 的斜率,进而可得直线
的斜率,进而可得直线![]() 的方程。(2)由直线
的方程。(2)由直线![]() ,
, ![]() 的方程可得点A的坐标,根据中点坐标公式可得外接圆圆心的坐标及半径,可得矩形
的方程可得点A的坐标,根据中点坐标公式可得外接圆圆心的坐标及半径,可得矩形![]() 外接圆的方程。(3)可判断点
外接圆的方程。(3)可判断点![]() 在圆外,且过点T的切线的斜率存在,由此设出切线方程,根据圆心到切线的距离等于半径可求得斜率,从而得到切线的方程。
在圆外,且过点T的切线的斜率存在,由此设出切线方程,根据圆心到切线的距离等于半径可求得斜率,从而得到切线的方程。
试题解析:
(![]() )由题意得直线
)由题意得直线![]() 的斜率
的斜率![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵ 点![]() 在直线
在直线![]() 上,
上,
∴ 直线![]() ,即
,即![]() .
.
(![]() )由
)由![]() ,解得
,解得![]() ,
,
∴ 点![]() ,
,
又点![]() ,
,
∴ ![]() 中点,即外接圆心为
中点,即外接圆心为![]() ,
,
又圆半径![]() ,
,
∴ 矩形![]() 的外接圆为
的外接圆为![]() .
.
(![]() )由条件得点
)由条件得点![]() 在圆外,且过点T的切线的斜率存在,设切线方程为
在圆外,且过点T的切线的斜率存在,设切线方程为![]() ,即
,即![]() ,
,
由直线和圆相切得圆心![]() 到切线的距离等于半径,
到切线的距离等于半径,
即 ,
,
整理得![]() ,
,
解得![]() 或
或![]() ,
,
当![]() 时,切线方程为
时,切线方程为![]() ,
,
当![]() 时,切线方程为
时,切线方程为![]() .
.
所以切线方程为![]() 或
或![]() 。
。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目