题目内容
椭圆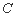 的中心为坐标原点
的中心为坐标原点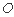 ,点
,点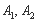 分别是椭圆的左、右顶点,
分别是椭圆的左、右顶点,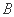 为椭圆的上顶点,一个焦点为
为椭圆的上顶点,一个焦点为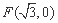 ,离心率为
,离心率为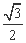 .点
.点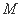 是椭圆
是椭圆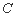 上在第一象限内的一个动点,直线
上在第一象限内的一个动点,直线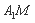 与
与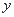 轴交于点
轴交于点 ,直线
,直线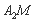 与
与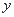 轴交于点
轴交于点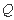 .
.
(I)求椭圆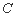 的标准方程;
的标准方程;
(II)若把直线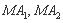 的斜率分别记作
的斜率分别记作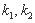 ,求证:
,求证: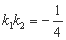 ;
;
(III) 是否存在点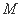 使
使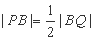 ,若存在,求出点
,若存在,求出点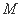 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
解: (I)由题意,可设椭圆C的方程为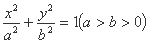 ,则
,则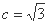 ,
,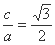 ,
,
所以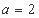 ,
,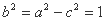 ,
,
所以椭圆C的方程为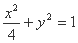 .
.
(II)由椭圆C的方程可知,点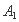 的坐标为
的坐标为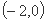 ,点
,点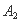 的坐标为
的坐标为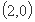 ,
,
设动点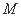 的坐标为
的坐标为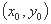 ,由题意可知
,由题意可知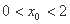 ,
,
直线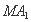 的斜率
的斜率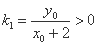 ,直线
,直线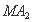 的斜率
的斜率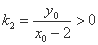 ,
,
所以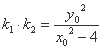 ,
,
因为点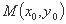 在椭圆
在椭圆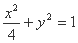 上,
上,
所以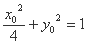 ,即
,即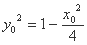 ,
,
所以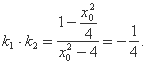
(III)设直线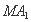 的方程为
的方程为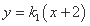 ,
,
令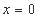 ,得
,得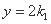 ,所以点
,所以点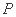 的坐标为
的坐标为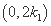 ,
,
设直线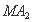 的方程为
的方程为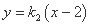 ,
,
令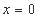 ,得
,得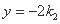 ,所以点
,所以点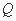 的坐标为
的坐标为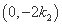 ,
,
由椭圆方程可知,点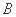 的坐标为
的坐标为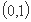 ,
,
由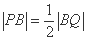 ,得
,得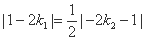 ,
,
由题意,可得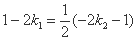
整理得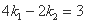 ,
,
与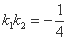 联立,消
联立,消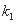 可得
可得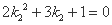 ,
,
解得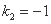 或
或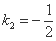 ,
,
所以直线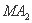 的直线方程为
的直线方程为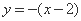 或
或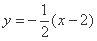 ,
,
因为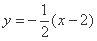 与椭圆交于上顶点,不符合题意.
与椭圆交于上顶点,不符合题意.
把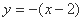 代入椭圆方程,得
代入椭圆方程,得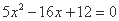 ,
,
解得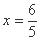 或
或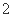 ,
,
因为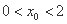 ,所以点
,所以点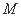 的坐标为
的坐标为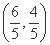 .
.
说明:解答题有其它正确解法的请酌情给分.

 阅读快车系列答案
阅读快车系列答案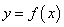 (
( )满足
)满足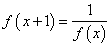 ,且当
,且当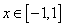 时,
时,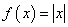 ,函数
,函数 ,则函数
,则函数 在区间
在区间 上的零点的个数为( )
上的零点的个数为( )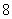 B.
B.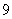 C.
C.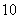 D.
D.
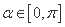 ,则方程
,则方程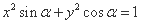 不能表示的曲线为
不能表示的曲线为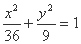 的弦被点(4,2)平分,则这条弦所在的直线方程是___________。
的弦被点(4,2)平分,则这条弦所在的直线方程是___________。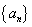 的各项均为正数,且
的各项均为正数,且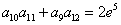 ,则
,则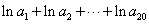 等于( )
等于( )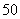 B.
B.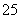 C.
C.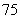 D.
D.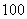
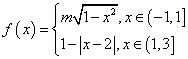 ,其中
,其中 ,且函数
,且函数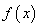 满足
满足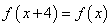 .若方程
.若方程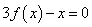 恰有
恰有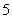 个根,则实数
个根,则实数 的取值范围是( )
的取值范围是( )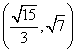 B.
B.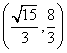 C.
C.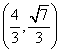 D.
D.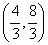
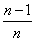 B.
B.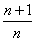 C.
C. 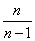 D.
D.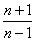
 个单位,所得图象关于轴对称,则
个单位,所得图象关于轴对称,则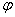 的最小值为( )
的最小值为( )