题目内容
3. 如图,在三棱柱ABC-A1B1C1中,底面△ABC是边长为2的等边三角形,D为AB中点.
如图,在三棱柱ABC-A1B1C1中,底面△ABC是边长为2的等边三角形,D为AB中点.(1)求证:BC1∥平面A1CD;
(2)若四边形BCC1B1是正方形,且A1D=$\sqrt{5}$,求直线A1D与平面CBB1C1所成角的正弦值.
分析 (1)连AC1,设AC1与A1C相交于点O,先利用中位线定理证明DO∥BC1,再利用线面平行的判定定理证明结论即可.
(2)推导出三棱柱ABC-A1B1C1是正三棱柱,以C为原点,CB为x轴,CC1为y轴,过C作平面CBB1C1的垂线为z轴,建立空间直角坐标系,利用向量法能求出直线A1D与平面CBB1C1所成角的正弦值.
解答 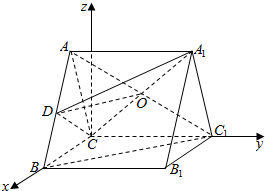 证明:(1)连AC1,设AC1与A1C相交于点O,连DO,则O为AC1中点,
证明:(1)连AC1,设AC1与A1C相交于点O,连DO,则O为AC1中点,
∵D为AB的中点,
∴DO∥BC1,
∵BC1?平面A1CD,DO?平面A1CD,
∴BC1∥平面A1CD.
解:∵底面△ABC是边长为2等边三角形,D为AB的中点,
四边形BCC1B1是正方形,且A1D=$\sqrt{5}$,
∴CD⊥AB,CD=$\sqrt{4-1}$=$\sqrt{3}$,AD=1,
∴AD2+AA12=A1D2,∴AA1⊥AB,
∵${A}_{1}{C}^{2}=4+4=8$,∴${A}_{1}{D}^{2}+C{D}^{2}={A}_{1}{C}^{2}$,
∴CD⊥DA1,又DA1∩AB=D,
∴CD⊥平面ABB1A1,∵BB1?平面ABB1A1,∴BB1⊥CD,
∵矩形BCC1B1,∴BB1⊥BC,
∵BC∩CD=C∴BB1⊥平面ABC,
∵底面△ABC是等边三角形,
∴三棱柱ABC-A1B1C1是正三棱柱.
以C为原点,CB为x轴,CC1为y轴,过C作平面CBB1C1的垂线为z轴,建立空间直角坐标系,
B(2,0,0),A(1,0,$\sqrt{3}$),D($\frac{3}{2}$,0,$\frac{\sqrt{3}}{2}$),A1(1,2,$\sqrt{3}$),
$\overrightarrow{{A}_{1}D}$=($\frac{1}{2}$,-2,-$\frac{\sqrt{3}}{2}$),平面CBB1C1的法向量$\overrightarrow{n}$=(0,0,1),
设直线A1D与平面CBB1C1所成角为θ,
则sinθ=$\frac{|\overrightarrow{{A}_{1}D}•\overrightarrow{n}|}{|\overrightarrow{{A}_{1}D}|•|\overrightarrow{n}|}$=$\frac{\frac{\sqrt{3}}{2}}{\sqrt{5}}$=$\frac{\sqrt{15}}{10}$.
∴直线A1D与平面CBB1C1所成角的正弦值为$\frac{\sqrt{15}}{10}$.
点评 本题考查线面平行的证明,考查线面角的正弦值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

| A. | 45°或135° | B. | 135° | C. | 45° | D. | 以上答案都不对 |
| A. | α∥β | B. | α⊥β | C. | α,β相交但不垂直 | D. | 以上均有可能 |
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
| A. | b<2$\sqrt{b-a}$ | B. | b>2$\sqrt{b-a}$ | C. | a<$\sqrt{b-a}$ | D. | a>$\sqrt{b-a}$ |